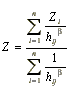Una vez seleccionada la zona de estudio, es necesario definir las variables ambientales que se usarán en la construcción del modelo de distribución. De acuerdo con los planteamientos anteriores, se establecerán relaciones entre la variable dependiente (vegetación) y un conjunto de variables independientes (el resto de variables ambientales).    Cada una de estas variables debe representarse de una forma numérica para su análisis estadístico. De entre las posibles formas de representación (modelos de datos) utilizables en un sistema de información geográfica, se ha elegido la estructura matricial por adaptarse especialmente bien a las necesidades del presente trabajo.    En este modelo de datos, las variables se representan mediante una matriz regular superpuesta al terreno. Cada celda, definida por su valor de fila y columna, posee el valor de la variable para su posición geográfica. La matriz regular es una de las estructuras posibles para los modelos digitales del terreno (MDT), definidos como estructuras de datos que representan la distribución espacial de una variable cuantitativa y continua (Felicísimo, 1994). El tamaño de la celda o tesela define la resolución espacial del MDT que, en nuestro caso, se ha fijado en 50 m de lado.
	La variable dependiente: los mapas forestales
	Los mapas forestales se obtienen a partir del mapa de vegetación actual (INDUROT, 1996a). A este mapa se le superpone la matriz que forma el MDT y se extrae la información sobre presencia/ausencia de cada formación forestal. La matriz resultante es binaria, codificándose con valor 1 la presencia de la formación que queremos estudiar y con 0 la ausencia. Lógicamente, se construye una matriz para cada una de las formaciones forestales a estudiar.    Las formaciones elegidas se encuentran descritas (Fernández, 1987 e INDUROT, 1997) y representadas cartográficamente como cinco mapas forestales, incluyendo algunos de ellos varias unidades fitosociológicas. Los mapas así representados son:
	Hayedos: Bosques dominados por el haya (Fagus sylvatica)  y encuadrados en la asociación Blechno spicanti-Fagetum sylvaticae. Abedulares: Bosques de abedul (Betula pubescens ssp. celtiberica) altimontanos oligótrofos encuadrables en la asociación Luzulo henriquesii-Betuletum celtibericae. Bosques mixtos oligótrofos: Bosques en los que participan fresnos (Fraxinus excelsior), arces (Acer pseudoplatanus), robles albares (Quercus petraea), etc. y que son incluibles en la asociación Luzulo henriquesii-Aceretum pseudoplatani. Robledales albares: Bosques oligótrofos con roble albar (Quercus petraea) y abedul (Betula pubescens ssp. celtiberica), en los cuales se reunen dos formaciones que cartográficamente se han separado únicamente en ciertos casos. Por una parte, se incluyen robledales albares con Luzula  sylvatica ssp.henriquesii y haya, incluibles en la asociación Luzulo henriquesii-Quercetum petraeae, de carácter netamente umbrófilo, y, por otra, robledales albares xerófilos, enmarcados en la asociación Linario triornithophorae-Quercetum petraeae. Rebollares: Bosques oligótrofos dominados por el rebollo (Quercus pyrenaica) e incluibles en la asociación Linario triornithophorae-Quercetum pyrenaicae.
	Estas formaciones forestales se han elegido por los dos motivos siguientes: Por su representatividad:  son las más representadas en la zona (suponen un 99% de la superficie arbolada del territorio). Por su origen: son climatófilas, su desarrollo se debe a las condiciones climáticas de la estación y no a situaciones edáficas locales.
	Las variables independientes: topografía, insolación y litología
	Las variables independientes, con la excepción de la litología, pueden ser modelizadas a partir de la información altimétrica recogida en el mapa topográfico. Las variables incluidas en el análisis se han seleccionado por  dos razones principales: Son variables potencialmente influyentes en la distribución de la vegetación ya que pueden ejercer de factor limitante sobre las distintas formaciones forestales. Son variables modelizables, es decir, su distribución de valores sobre el terreno puede ser estimada por diferentes métodos a partir de información disponible (mapa topográfico y litológico)    Las variables consideradas son las siguientes:
	Altitud: elevación del terreno sobre el nivel del mar. Pendiente: gradiente o tasa de cambio de la altitud. Curvatura: concavidad / convexidad del terreno o tasa de cambio de la pendiente. Insolación potencial: tiempo durante el cual cada lugar recibe radiación solar directa en una época del año determinada en ausencia de nubosidad. Litología: naturaleza litológica del sustrato.
	La altitud: el modelo digital de elevaciones
	El modelo digital de elevaciones o MDE representa la altitud del terreno. Para su elaboración se ha utilizado la topografia existente, en distintos formatos: Para la zona incluida en las hojas 75 y 100 del Mapa Topográfico Nacional de España, se ha utilizado la cartografía altimétrica digital elaborada por el Servicio Geográfico del Ejército a escala 1:50.000 con un intervalo entre curvas de nivel de 20 metros. Para el resto (cabecera del río Narcea) se digitalizaron manualmente las curvas de nivel y puntos acotados necesarios a partir del mapa impreso correspondiente a la hoja 101 del mismo servicio cartográfico.   Las dos bases topográficas, con el mismo nivel de resolución, son comprobadas y casadas, creando una única base topográfica compuesta por curvas de nivel y puntos acotados.   El MDE se ha construido utilizando un método de interpolación mediante el inverso de la distancia ponderada (IDP), este metodo, asigna a cada celda o tesela del territorio un valor de altitud estimado a partir de todos los puntos situados en un círculo de 250 m de radio, ponderando cada dato en función inversa del cuadrado de la distancia. La expresión de cálculo se muestra en la Ecuación 1. Ecuación 1.    Donde Z es la altitud del punto problema; Zi representa la altitud del punto i del conjunto de los n usados como datos, de altitud conocida; hij es la distancia de cada dato al punto problema y, finalmente, B es el coeficiente que permite ponderar la influencia de la distancia en la interpolación; en este caso  B=2.    Gráficamente, el MDE puede representarse codificando las altitudes en tonos de gris, de forma que los tonos más claros corresponden a las zonas más elevadas y las zonas más oscuras a los puntos de menor altitud. La distribución de altitudes puede representarse mediante un histograma donde se ve la distibución de las mismas.
	La pendiente: el modelo digital de pendientes
	A partir del MDE es posible estimar la pendiente que corresponde a cada celda del modelo valorando la tasa de cambio de la altitud. El SIG utilizado realiza este cálculo directamente mediante el operador de Sobel (James, 1988) que estima la pendiente de una celda en función de la altitud propia y de sus 8 vecinos más próximos.    El resultado que se obtiene con la aplicación de esta función a cada celda es el modelo digital de pendientes (MDP), una matriz estructuralmente igual al MDE pero en la cual cada celda recoge un valor de pendiente estimado.    Gráficamente, el MDP puede representarse codificando en tonos claros las pendientes más fuertes y en tonos oscuros las zonas de menor pendiente. Así mismo, es posible representar graficamente una distribucion de las frecuencias de cada clase de pendiente en la zona de estudio.
	La forma: el modelo digital de curvatura
	El modelo digital de curvatura (MDC), se obtiene también a partir del MDE analizando la tasa de cambio de la pendiente. El MDC recoge la forma topográfica en el entorno de cada celda: concavidad, planeidad o convexidad.    La curvatura se estima en función de la derivada segunda de la altitud. El SIG utilizado provee una función que crea el MDC directamente ajustando un polinomio de cuarto grado a la superficie de 3 x 3 celdas representada por el punto problema y sus 8 vecinos más próximos. El operador se denomina laplaciano (James, 1988); los resultados negativos indican zonas cóncavas, los positivos zonas convexas y los nulos zonas planas. En la zona de estudio, los valores oscilan entre -9,7 y 5,7 indicando una fuerte variación en la rugosidad del terreno. Los valores típicos para estos modelos, van de valores de -1 a 1 en zonas de relieve de colinas suaves hasta valores de -4 a 4 en zonas montañosas. Los valores más altos indican variaciones muy fuertes del relieve.    La representación gráfica del MDC se ha realizado codificando en tonos oscuros las zonas convexas y en tonos claros las cóncavas tal y como se puede ver en la imagen.
	La radiación solar: los modelos digitales de insolación
	Se define como insolación potencial en un punto al tiempo que está sometido a la radiación solar directa en una época determinada del año en ausencia de nubosidad. La insolación potencial depende básicamente de tres factores: Latitud geográfica: positiva en el hemisferio Norte y negativa en el Sur. La trayectoria solar: función de la época del año, representada por el valor de declinación solar. Efecto de sombra: inducida por la topografía del entorno y dependiente del factor anterior. De lo expuesto se deduce que es posible construir diferentes modelos digitales de insolación (MDI), para cada época del año. En este trabajo se han construido cinco modelos diferentes, representativos de diversas épocas del año caracterizadas por un valor medio de declinación solar. Los periodos se han elegido según Heywood (1964), tal como se muestra en la tabla siguiente:
	Declinación solar Efeméride astronómica y fecha central Días representados Máxima insolación Mínima insolación Modelo creado Imagen -22,5º Solsticio de invierno: 21 de Diciembre 45 8 h 50 min 0 min MDI (D=-23º) -12,5º Intermedio entre el equinoccio de otoño y el solsticio de invierno 44 10 h 30 min 0 min MDI (D=-12º) 0º Equinoccios de primavera y otoño: 21 de Marzo y 21 de Septiembre 91 12 h 10 min 0 min MDI (D=0º) +12,5º Intermedio entre el equinoccio de primavera y el solsticio de verano 46 13 h 30 min 50 min MDI (D=12º) +22,5º Solsticio de verano: 21 de Junio 48 15 h 10 min 2h 30 min MDI (D=23º)
	La construcción de los MDI se realiza simulando la trayectoria solar para cada época del año y analizando la existencia o no de sombreado sobre cada celda. Al final del día se tiene una suma del tiempo que cada celda está expuesta a la radiación solar. El cálculo se ha realizado para intervalos de tiempo de 10 minutos, lo que aporta una precisión suficiente para la modelización.    En cada modelo se presentarán valores de insolación potencial entre un mínimo de cero (celdas en sombra durante todo el día) y un máximo dependiente de la duración del día en cada época del año. La Tabla anterior muestra una síntesis de los valores obtenidos.    Los distintos MDI se representan gráficamente en tonos de gris, donde la zonas con mayor insolación potencial se representan en tonos más claros.   Un análisis somero de estos modelos nos muestra que la insolación potencial es muy diferente de un lugar a otro y de una época del año a otra. Así, aparecen zonas que reciben radiación de forma más o menos constante durante todo el año y que se corresponde con estaciones con exposición Sur o localizadas en las zonas de mayor altitud y, por tanto, sin apantallamiento topográfico. En estas últimas, la radiación incidente puede superar a la duración teórica del día; esto es debido a que, en las zonas más altas, el sol puede incidir minutos antes del orto y después del ocaso oficial. Otras estaciones, en cambio, permanecen buena parte del año en umbría, recibiendo únicamente la radiación proveniente de la reflexión de zonas cercanas y no valorada en este modelo.   La interpretación de los MDI nos puede dar más información que la simple radiación incidente en cada punto. Las zonas más umbrías se corresponden, por lo general, con zonas más húmedas y donde la evapotranspiración es menor. En las zonas más expuestas, la evapotranspiración es mayor y la humedad edáfica menor, descendiendo la tasa de reciclado de la materia orgánica. Además, en las zonas de mayor altitud y con fuerte incidencia solar en invierno, los cambios de temperatura en el ciclo día-noche son más acusados, produciéndose procesos de gelifracción en el suelo que pueden afectar directamente a la vegetación.
	El sustrato: el mapa litológico
	El mapa litológico utilizado se ha sintetizado a partir del mapa litologico escala 1:25.000 (INDUROT,1996b) sobre una matriz donde a los terrenos de naturaleza predominantemente silícea les corresponde el valor 0 y a los de naturaleza predominantemente calcárea o mixta el valor de 1. Este agrupamiento de unidades se justifica ya que nos interesa la riqueza del suelo y no la naturaleza o edad concreta del sustrato. Bajo este punto de vista se puede interpretar que sobre materiales carbonatados o mixtos los suelos formados son más ricos que sobre materiales de naturaleza silícea del tipo de las cuarcitas, areniscas o pizarras.