El modelo de distribución

La regresión logística

   La regresión logística es un método estadístico que se utiliza para describir la relación entre una variable dependiente Y, y una o más variables independientes X1, X2,...,Xn (Kleinbaum, 1994; Jovell, 1995). En el caso de que aparezcan varias variables independientes nos encontramos ante un caso de regresión logística multivariante (RLM) cuyas principales características son las siguientes:

  • Describe la función logística, una función cuyo valor, f(z) responde a una expresión no lineal de la siguiente forma:

f(z) = 1 / (1 + e -z)

               Ecuación 2
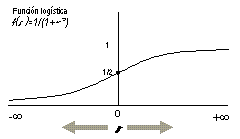Forma de la curva resultante de la función logística. Los valores f(z) varían entre 0 y 1. Puede fijarse un valor umbral para separar los valores de probabilidad en dos clases: idóneo / no idóneo. En la figura, este valor umbral se ha fijado en 0,5 (1/2)

  • La variable dependiente es dicótoma y admite valores muestrales de 0 o 1.
  • El modelo logístico produce valores de f(z) continuos en el rango 0 - 1, lo que hace que sea un modelo apropiado para describir valores de probabilidad.
  • No es necesario que las variables independientes sean continuas sino que pueden ser nominales o incluso dicótomas.
  • No es necesario que las variables independientes tengan una distribución normal.

  El modelo logístico es adecuado para el problema que nos ocupa debido a que calcula los coeficientes de un modelo probabilístico, constituido por el conjunto de variables independientes que mejor pronostica el valor de una variable dependiente dicotómica. Es decir, nos permite establecer una función dependiente de las variables modelizadas, con unos valores de salida que expresan valores de probabilidad, a la vez que acepta valores de entrada dicótomos y nominales. Así, al aplicar el modelo logístico, obtenemos la función de idoneidad para cada una de las formaciones boscosas estudiadas en cada una de las teselas. El resultado es un nuevo MDT que expresa los valores de probabilidad de desarrollo de cada una de las formaciones en cada una de las celdas.

   Para aplicar la función logística, es preciso calcular el modelo logístico a partir de una combinación de las variables independientes incluidas en el modelo de la siguiente forma:

Ecuacion 3              Ecuación 3

   El calculo de los coeficientes se realiza a través de una muestra tomada de la realidad, en la cual se incluyen tanto casos positivos como negativos para la variable a considerar. La aplicación de este modelo sobre la vegetación real (excluidos los puntos de la muestra) permite establecer la idoneidad del modelo a través de una matriz de confusión, (Kleinbaum, 1994) en la cual, se comparan los valores reales con los valores predichos por la regresión:

Presencia estimada

No

Si

Total

Presencia real

No

F11

F12

T1

Si

 F21

F22

T2

TOTAL

T3

T4

T

  En la matriz de confusión, F11 y F22 representan los aciertos del modelo, es decir, presencia de cierta formación forestal donde realmente existe y ausencia de la misma donde realmente no la hay. Los errores del modelo se representan en las celdas F12 y F21, pero el significado de ambos es diferente; F12 es el error por comisión, puntos donde se acepta la existencia de una formación cuando realmente no existe, es decir, las zonas en las que se potencia la formación leñosa por tener las condiciones ambientales adecuadas. La celda F21, denominada error por omisión, muestra los puntos en los cuales, aún existiendo la formación, ésta no se potencia por poseer aparentemente condiciones inadecuadas. Si el modelo es adecuado, este error debe ser bajo.

La selección de las muestras

  El análisis por medio de la regresión logística multivariante se basa en una muestra de la población, a partir de la cual se calculan los estadísticos muestrales y se estiman los parámetros aplicables a la población. En nuestro caso, la población corresponde al total de celdas que cubren el territorio. La selección de las muestras se ha realizado mediante un muestreo aleatorio del 10% del total de celdas; posteriormente se ha seleccionado el mismo número de celdas con casos positivos (formación forestal presente) como negativos (formación forestal ausente). El muestreo aleatorio asegura que la representación (distribución de frecuencias) de los distintos factores ambientales es similar en la muestra y en la realidad.

   El resultado de la operación es una muestra para cada formación forestal. El tamaño de la misma depende de la representación de dicho bosque sobre el terreno. Las muestras se recogen en archivos de texto donde se especifica para cada punto la presencia o ausencia de la formación forestal y los valores de las diferentes variables independientes en el formato adecuado para ser introducidas en un programa de tratamiento estadístico.

Cálculo del modelo logístico

  Para el cálculo de la regresión logística se siguieron dos vías diferentes. Inicialmente, se utilizó una de las herramientas que incorpora el SIG utilizado, que permite calcular los coeficientes de la RLM así como un estadístico de significación. Sin embargo, este método no permite utilizar variantes algo más sofisticadas que analizan las diversas combinaciones de variables hasta determinar aquélla que con el mínimo de elementos permite una explicación máxima de la varianza.

   El método utilizado finalmente, denominado STEPWISE, selecciona las variables una a una partiendo de la constante e introduciendo en el modelo la variable que menor significación tiene en cada paso, comprobando cada vez que se introduce una nueva variable que las demás cumplan las condiciones de eliminación. Este método fue utilizado mediante una aplicación estadística comercial, exportando los ficheros muestrales al formato adecuado.

Creación de los modelos de distribución potencial

  El modelo logístico calculado para cada formación forestal a partir de las muestras se aplica a la totalidad de las celdas del territorio. A cada una de ellas se le asigna un valor de idoneidad en función de los valores de las variables independientes o descriptoras utilizadas. El valor de idoneidad está en el rango 0-1: los valores próximos a 0 indican que las variables ambientales hacen el lugar poco adecuado para el desarrollo de la formación forestal analizada; los valores próximos a la unidad señalan localizaciones donde la combinación de valores ambientales es idónea para el establecimiento del bosque considerado.