| Felicísimo, Angel M.; García-Manteca, Pilar (1990): Corrección del efecto topográfico en las imágenes Landsat mediante el uso de un modelo digital de elevaciones. III Reunión Científica del Grupo de Trabajo en Teledetección: 209-216. Madrid, 1989. |
CORRECCIÓN DEL EFECTO TOPOGRÁFICO EN LAS IMAGENES LANDSAT MEDIANTE EL USO DE UN MODELO DIGITAL DE ELEVACIONES
Resumen
Los procesos de identificación, clasificación y comparación multitemporal de imágenes de satélite se ven dificultados por los efectos de iluminación y sombreado debidos a orientación de las laderas frente al vector solar, especialmente importantes en zonas montañosas. Se presenta un método simple que, a partir de un modelo digital de elevaciones, de los valores de iluminación directa y difusa, y de las coordenadas solares en el momento de la toma de la imagen, construye un modelo de reflectancia en el que los valores son función de la exposición de cada punto frente a las fuentes de iluminación. El modelo supone superficies perfectamente difusoras y tiene en cuenta el posible ocultamiento topográfico. Los valores calculados para cada punto son utilizados para una corrección de las imágenes Landsat TM (bandas 4 y 5), previamente rectificadas geométricamente al sistema de proyección UTM. La corrección, realizada pixel a pixel, es proporcional a la desviación del valor calculado frente al de una superficie horizontal.
Abstract
Identification, classification and comparison of multitemporal satellite data become difficult due to illumination and shadow effects produced by hillside orientation in relation to the sun, specially in mountainous areas. From a digital elevation model, the values of direct and diffuse illumination and the sun coordinates, a simple method is presented to build up a terrain reflectance model. The scene radiance values are calculated as a function of surface orientation and the distribution and weight of two light sources: collimated for the solar direct radiation and hemispheric for the diffuse component. The model assumes perfectly diffuse (Lambertian) surfaces and takes into account the topographic screening. The reflectance model is used for the radiometric correction of a Landsat Thematic Mapper image, previously rectified to UTM projection. The correction is proportional to the data deviation of each pixel from the calculated value for the horizontal surface.
1. Introducción
Los métodos de teledetección permiten obtener una información sobre la superficie del terreno complementaria de la cartografía temática convencional. La combinación de ambos tipos de datos no es inmediata ya que las imágenes de satélite presentan unas características, inherentes a los métodos de captación, que dificultan la extracción directa de información sobre los tipos de suelo y su cubierta vegetal. Una buena interpretación de los datos de las imágenes requiere una corrección previa al análisis,tanto geométrica como radiométrica.
La distorsión geométrica implica realizar una corrección que persigue la restitución de la imagen de acuerdo con un sistema de proyección geográfica determinado. Los métodos para realizar esta corrección dependen del grado de distorsión, moderado en el caso de los satélites de la serie Landsat.
Por otra parte, la iluminación oblicua y una topografía irregular genera unos efectos de sombreado e iluminación que modifican la respuesta debida exclusivamente al tipo de superficie. El efecto topográfico provoca un variación de la respuesta radiométrica de la superficie inclinada frente a la de una horizontal. Esta es función de su posición (pendiente y orientación) frente a las fuentes de iluminación y al observador. Otro efecto importante es el ocasionado por el ocultamiento topográfico, es decir, el sombreado producido por el entorno sobre un punto del terreno para la posición del sol en el momento de la toma de la imagen.
El problema de la corrección radiométrica de los datos procedentes de un sensor multiespectral se centra, por tanto, en la determinación de la respuesta característica de los diferentes tipos de superficie manteniendo invariante el efecto debido a la topografía y posiciones del sol y del observador.
En las páginas siguientes, se expone el método desarrollado para la solución de este problema, basado en una simulación de las condiciones de formación de la imagen que tiene en cuenta los factores influyentes principales: condiciones de iluminación y topografía.
El trabajo se desarrolla en el Parque Natural de Somiedo, un área del Suroeste de Asturias (Figura 1), con una extensión próxima a los 300 km2 y un relieve especialmente abrupto. La pendiente media es de 24º (45%), y las altitudes se distribuyen entre una cota mínima de 400 m en el extremo septentrional y cumbres superiores a los 2.100 m en la divisoria meridional. La altitud media del área es de 1300 m.
El área estudiada pertenece geológicamente a la unidad del Manto de Somiedo, una de las más occidentales de la Zona Cantábrica. La naturaleza de los materiales es muy variada, así como la propia estructura interna de la unidad. El trazado general de todas las estructuras en el Parque es NO-SE, con una fuerte incurvación hacia el Norte, donde las capas llegan a disponerse en dirección SO-NE.
La vegetación de la zona es también muy variada, función de la diversidad geológica, el relieve y la influencia humana. Predominan los hayedos, robledales y encinares entre las formación de bosque, y los matorrales calcícolas, brezales y piornales entre las formaciones arbustivas. Los prados alcanzan una extensión importante, motivada por la economía básicamente ganadera de la zona, ocupando preferentemente las zonas de poca pendiente en altitudes medias y bajas.
Figura 1.– Situación del Parque Natural de Somiedo, en el SO de Asturias.
El área de estudio fue elegida tanto debido a su diversidad geológica y vegetal, como por su relieve actual. El levantamiento alpino del bloque cantábrico condujo al encajamiento de la red hidrográfica y, consecuentemente, a un rejuvenecimiento de las anteriores estructuras. Los cauces fluviales más importantes, los ríos Somiedo y Pigüeña, se disponen en dirección N-S, discurriendo desde el eje de la Cordillera hacia las zonas bajas, atravesando diferentes conjuntos litológicos. Los cauces restantes (Pigüeces, Las Morteras, Saliencia, Valle, etc.) discurren aprovechando los materiales menos competentes, en direcciones coincidentes con las estructuras hercinianas (Marquínez y Suarez, 1986). Las pendientes en las laderas de los valles son elevadas, y el ocultamiento topográfico adquiere gran importancia en la mayoría del período anual, con amplias zonas de umbría y fuertes contrastes de exposición a la radiación solar.
2. Métodos
2.1. Integración de la imagen TM y el modelo digital de elevaciones
La altitud es una variable que puede ser descrita mediante un conjunto de valores puntuales, formando un modelo digital de elevaciones (MDE). En los MDE, los valores puntuales pueden ser tratados de una forma análoga a los valores digitales de una imagen de satélite. En un MDE compuesto por una matriz rectangular de altitudes, las distancias que separan los datos son equivalentes al tamaño del pixel; consecuentemente, la resolución del modelo será proporcional a la densidad de la red de altitudes. Este tipo de datos es susceptible de manipulaciones numéricas y visuales análogas a las utilizadas en el tratamiento de imágenes convencionales. Un MDE puede ser presentado en una pantalla gráfica traduciendo las altitudes a un valor concreto de brillo mediante una transformación de escala adecuada.
El MDE utilizado en el presente trabajo está formado por un conjunto de 202732 cotas, distribuidas en una matriz cuadrada de 512 x 512 elementos. La distancia entre filas y columnas de datos es de 25 m. El modelo representa un área de 12,8 x 12,8 km que incluye el sector SE del Parque, con los valles de los ríos Saliencia, del Valle y Somiedo. Los puntos del MDE exteriores a los bordes del Parque, sobre los que no existen datos de altitud, se han identificado con el valor específico, lo que es tenido en cuenta por los programas si procede un tratamiento especial de los límites.
La imagen utilizada (203/030) corresponde al sensor Thematic Mapper del Landsat 5. Fue tomada a las 10.30 h (TMG) del 21 de junio de 1986. A esta fecha y hora le corresponden unos valores de acimut solar y elevación sobre el horizonte de 122.3 y 56,1º respectivamente.
La imagen original fue rectificada geométricamente para su superposición al MDE, adoptando un tamaño de pixel de 25 m. Este tamaño de pixel parece adecuado para el remuestreo de la imagen TM sin una pérdida sensible de resolución, dado que el pixel original tiene una dimensión nominal de 30 x 30 m. La asignación de los valores a cada pixel se realizó directamente, por el método del vecino más próximo, pues se consideró innecesario acudir a otros métodos de interpolación dados los objetivos del trabajo. El sistema de proyección geográfica elegido fue el UTM. Las correcciones geométricas se realizaron mediante funciones polinómicas de segundo grado, basadas en un mínimo de 9 puntos de control localizados con precisión. En todos los casos, el error máximo en la estimación de coordenadas ha sido menor que el tamaño de pixel utilizado.
El proceso de las imágenes y modelos digitales ha sido realizado íntegramente en un microordenador IBM-AT con tarjeta gráfica DT-2871, mediante programas desarrollados en el INDUROT (Universidad de Oviedo).
2.2. El modelo de reflectancia
Para algunas superficies, la fracción de radiación reflejada hacia el sensor depende básicamente de su orientación frente al vector solar. La modelización de esta variable puede realizarse conociendo la pendiente y orientación de cada punto de la zona, los valores de acimut y elevación solares y del observador (sensor) y la relación entre las componentes difusa y directa de la radiación solar. La componente directa de la radiación debe ser corregida en aquellas zonas donde exista ocultamiento topográfico, por lo que éste debe ser valorado para su inclusión en el modelo.
Un modelo digital del terreno puede ser expresado como un conjunto
de valores Z(x,y) donde Z es la variable considerada (altitud en un MDE)
del punto de coordenadas (x,y). De forma equivalente, el modelo de reflectancia
asigna un valor L(x,y) a cada punto del terreno. El valor de L depende
básicamente de las variables siguientes:
En cada punto, el vector normal a la superficie del terreno puede ser calculado mediante el producto de los vectores [1,0,p] y [0,1,q], donde p y q son respectivamente las pendientes en sentido E-O y S-N (Woodham y Gray, 1987). El par de valores (p,q) se denomina gradiente y debe ser calculado para cada punto del modelo de reflectancia.
Este cálculo se realiza a partir del MDE mediante las expresiones siguientes:
p(x,y) = ¶ f(x,y)/¶ x = [f(x+1,y) – f(x–1,y)] / 2D x
q(x,y) = ¶ f(x,y)/¶ y = [f(x,y+1) – f(x,y–1)] / 2D y
donde D x y D y representan la distancia entre los datos del MDE en las mismas unidades que f(x,y). El gradiente está formado, por tanto, por los valores de las derivadas parciales de la altitud respecto a los ejes X e Y. El cálculo se realiza mediante una ventana de 3 x 3 centrada en cada pixel del MDE.
Los valores de pendiente (PE) y orientación (OR) pueden derivarse de los del gradiente mediante las expresiones (Franklin, 1987):
tg PE = sqrt (p2+ q2)
tg OR = –q / –p
En el caso del vector solar, se conocen generalmente las coordenadas esféricas: acimut (AZ) y altura sobre el horizonte (AL). Llamando AS al complementario de AL, el gradiente de una superficie perpendicular al vector solar viene dado por (Woodham y Lee, 1985):
ps = –cos AZ · tan AS
qs = –sin AZ · tan AS
Teniendo en cuenta las consideraciones anteriores, el modelo de reflectancia, que asigna un valor L a cada punto de coordenadas (x,y), puede expresarse de la forma siguiente:
L(x,y) = R(p,q)
donde R es el valor de reflectancia asignado a una superficie de gradiente
(p,q) frente al vector solar (ps, qs). Los valores de R pueden calcularse
directamente a partir del MDE y una vez definidos los valores del gradiente
para el vector solar (Horn y Sjoberg, 1979):
R(p,q) = E0/p · a · (n / (d1 · d2)) donde
n = 1 + (p·ps) + (q·qs)
d1 = sqrt(1+p2+q2)
d2 = sqrt(1+ps2+qs2)
donde el último factor representa el coseno del ángulo
i, formado por el vector solar y la normal a la superficie del terreno
(figura 3). Si cos i < 0 debe tomarse R(p,q) = 0 (situación
de autoocultamiento).
R(p,q) = L0/2 · a · (1 + 1/sqrt(1+p2+q2))
donde el último término representa el coseno del ángulo e (figura 3), y L0 es la radiancia de la fuente hemisférica de iluminación. El ángulo e es el formado por la normal a la superficie y la línea visual del observador.
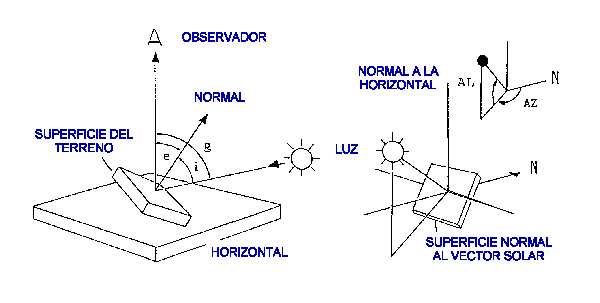
Figura 2.– Convenciones geométricas utilizadas en el texto:
i = Angulo formado por el vector solar y la normal a la superficie
e = ángulo formado por la normal a la superficie y la línea
visual (sensor, coincidente con el eje Z)
g = ángulo formado por el vector solar y la línea visual
AL = altura del sol sobre el horizonte (AS = 90º – AL)
AZ = acimut solar, medido en sentido horario desde el Norte (0º)
La superficie normal al vector solar tiene por gradiente (ps, qs) :
ps = –cos AZ . tan AS
qs = –sin AZ . tan AS
El modelo de reflectancia final es una composición de las dos componentes anteriores, una vez ponderada su aportación en función del porcentaje de radiación directa y difusa estimado para la zona.
Han sido construidos tres modelos con diferentes porcentajes: 80/25, 85/15 y 95/5 por ciento, respectivamente. En el Observatorio Meteorológico de Oviedo, los porcentajes observados para la misma fecha y hora fueron del 81 y 19%. La componente difusa de la radiación produce en la práctica un efecto suavizador de los contrastes debidos al relieve. El mejor resultado se ha observado para la combinación de componentes 80/20 (la más próxima a las medidas del Observatorio de Oviedo), mientras que el resto provoca una sobrecorrección en las zonas donde el valor de cos i está próximo a cero.
La componente directa debe modificarse en las áreas de ocultamiento topográfico, en las que sólo tiene influencia la componente difusa. Para ello es necesario un método de detección de áreas en sombra basado en algoritmos de eliminación de superficies ocultas.
El método utilizado (Fernández y Felicísimo, 1987) consiste esencialmente en la generación de un perfil topográfico, sobre la línea de azimut solar, en cada punto del MDE. A intervalos regulares, coincidentes con la distancia entre filas y columnas (25 m) se comprueba si la altura en el perfil es suficiente para interceptar el vector solar, definido por el ángulo de elevación sobre el horizonte. En caso positivo, sólo se tiene en cuenta la componente difusa de la radiación. En caso negativo, se suman las dos componentes de la radiación global para componer el modelo de reflectancia.
La comprobación de ocultamiento se realiza dentro de un entorno limitado de cada punto del modelo digital, definido en función de la altura máxima del MDE y del ángulo de elevación solar. El modelo de ocultamiento es un mapa binario, en el sentido de que puede ser expresado por dos únicos valores: 0 si existe ocultamiento y 1 si no existe. Una vez generado, se realiza una multiplicación pixel a pixel por el modelo de reflectancia por radiación directa para incluir el efecto de sombra.
En el caso de la imagen TM, las zonas en sombra detectadas a las 10.30 h son mínimas, por lo que el modelo de reflectancia no se ve apenas modificado. En el caso de épocas del año menos próximas al solsticio de verano o de horas más lejanas del mediodía, la influencia del ocultamiento topográfico puede ser muy importante.
2.3. Corrección radiométrica de la imagen TM
El mapa de reflectancia construido es un modelo idealizado que asume un albedo constante para toda la superficie del terreno. Los valores de reflectancia calculados se suponen debidos exclusivamente a los factores topográficos y de posición de las fuentes de luz y del observador.
Llamando RM(h) al valor de reflectancia estimado para una superficie horizontal (p = q = 0), y si. RM(i), es el correspondiente a un punto i del terreno, el cociente RM(h)/RM(i) = k(i), es una estimación del efecto topográfico para ese punto. El valor de k(i) puede ser mayor, igual o menor que la unidad, en función del valor del gradiente frente a las fuentes de luz y de la existencia de sombra en el punto i. Valores menores que 1, por ejemplo, sugieren una orientación preferente hacia la fuente de luz direccional y ausencia de ocultamiento topográfico.
Si se toman los valores digitales reales de la imagen Landsat RL(i), la corrección de la reflectancia para eliminar el efecto topográfico se realiza de forma automática:
RL'(i) = RL(i)· k(i) = RL(i) · RM(h)/RM(i)
donde:
RL'(i) : valor corregido en la imagen para
el pixel i,
RL(i) : valor observado en la imagen para el pixel i,
RM(h) : valor modelizado para una superficie horizontal
RM(i) : valor modelizado para el pixel i.
Aplicando esta transformación, el valor observado para cada pixel se aumenta o disminuye proporcionalmente al efecto topográfico modelizado a partir del MDE. La imagen resultante continúa teniendo fuertes variaciones de reflectancia pero ya debidas en una mayor proporción al cambio de características de la superficie y no al diseño topográfico.
El proceso se ha aplicado a las bandas 4 y 5 del sensor TM.

Arriba se muestra una imagen sin corrección radiométrica. La zona no corresponde a la del trabajo original debido a que las imágenes correspondientes son irrecuperables.Se ha decidido incluir otras alternativas para mostrar el efecto visual del proceso. Abajo se muestra la misma imagen tras la corrección presentada en el texto.

3. Discusión
Los problemas que se plantean en la realización de la corrección propuesta son varios, de naturaleza práctica y metodológica. Un problema práctico importante es la necesidad de disponer de un modelo digital de elevaciones de la zona estudiada, con una resolución espacial comparable al tamaño de pixel de la imagen rectificada. Cabe suponer, sin embargo, que la disponibilidad de los MDE sea cada vez más general, debido a la necesidad paralela de integrar la información altimétrica en los Sistemas de Información Geográfica, actualmente en desarrollo en muchos lugares.
El modelo de reflectancia se construye a partir de varias hipótesis simplificadoras. Una de ellas es que la reflexión del terreno se hace de forma perfectamente difusa (lambertiana). En este caso, la reflectancia depende exclusivamente del ángulo formado por el vector solar y la normal a la superficie.
Una opción alternativa es suponer la reflexión parcialmente dependiente del ángulo de visión, formado por el eje visual y la normal a la superficie (superficies de Minnaert). En este caso, las funciones de reflectancia adoptan formas diferentes, dependientes de los ángulos i, e y de un coeficiente k cuyo valor está comprendido entre cero y la unidad (Woodham y Lee, 1985). La superficie lambertiana es un caso extremo, en el que k = 1.
La adopción de superficies de Minnaert trae consigo la necesidad de fijar un valor al parámetro k. Este parámetro se muestra en la práctica dependiente, no sólo del tipo de superficie, sino también de la longitud de onda de la luz y de las coordenadas del vector solar (Woodham y Lee, 1985). La complejidad de manejar este conjunto de variables parece excesiva a la hora de realizar un modelo de validez general. Por este motivo se ha elegido finalmente la opción de considerar la superficie perfectamente difusora.
Las proporciones correctas de las componentes directa y difusa de la radiación incidente deben ser estimadas de forma aproximada. Una vía para ello consiste en relacionar la reflectancia aparente de los puntos en sombra con su pendiente, deducible del modelo digital de elevaciones. En el caso presente, los puntos del modelo que sufren ocultamiento topográfico son demasiado escasos para permitir una evaluación adecuada, por lo que las proporciones han sido sólo aproximadas. Como ya se ha indicado,los porcentajes 80/20 por ciento han ofrecido buenos resultados, mientras que proporciones menores de la componente difusa han provocado sobrecorrecciones para las zonas más oscuras del modelo.
En este trabajo, la valoración de los resultados es solamente subjetiva, derivada de la observación visual de las imágenes anteriores y posteriores a la corrección. Una valoración objetiva puede basarse en ensayos de clasificación partiendo de las mismas áreas-muestra, representativas de los diferentes recubrimientos del suelo. Desde la experiencia actual cabe esperar una mejora en los procesos de identificación y clasificación, especialmente con el uso de imágenes multitemporales, en las que las diferencias de reflectancia aparente debidas a la posición solar pueden ser muy importantes.
Agradecimientos
Este trabajo ha sido realizado mediante una Subvención de Proyectos de Investigación de Temática Asturiana, concedida por la Universidad de Oviedo en la convocatoria de 1988.
Agradecemos a Angel Martínez Nistal, del Centro de Proceso de Imágenes de la Universidad de Oviedo, su continua y desinteresada ayuda, sin la cual una parte de este trabajo no habría podido realizarse.
Bibliografía
Fernández, G.; Felicísimo, A.M. 1987. Método de cálculo de la radiación incidente en áreas con apantallamiento topográfico. Revista de Biología de la Universidad de Oviedo, 5: 109-119.
Franklin, S.E. 1987. Geomorphometric processing of digital elevation models. Computer & Geosciences, 13(6): 603-609.
Horn, B.K.P.; Sjoberg, R.W. 1979. Calculating the reflectance map. Applied Optics, 18(11): 1770- 1779.
Marquínez, J.; Suárez, A. 1986. Geología. En Estudio Ambiental del Concejo de Somiedo. J. Marquínez García (Ed): 90-123. Universidad de Oviedo. Oviedo.
Woodham, R.J. and Gray, M.H. 1987. An analytic method for radiometric correction of satellite multispectral scanner data. IEEE Transactions on Geoscience and Remote Sensing, 25 (3): 258-271.
Woodham, R.J. and Lee, T.K. 1985. Photometric method for radiometric correction of multispectral secanner data. Canadian Journal of Remote Sensing, 11 (2): 132-161.
