 |
 |
|
Parte 7 |
| La rugosidad |
|
|
Al contrario de lo que ocurre con la pendiente, la orientación
y la curvatura, no existen criterios uniformes para llevar a cabo la medida
de la rugosidad. Diversos autores han aplicado
métodos significativamente distintos para su evaluación; por
ejemplo, Balce (1987:324) utiliza la pendiente media como estimador de un
factor de rugosidad. Evans (1972:27-33) realiza una revisión de
métodos, entre los cuales menciona desde rangos de altitud hasta la
desviación estándar de la elevación en entornos limitados.
Hobson (1967, 1972) propone que, dado un punto del terreno, se calculen los
vectores unitarios perpendiculares a la superficie en él y en los
puntos de su entorno. Si el terreno es uniforme la suma
vectorial será elevada y la dispersión baja; en el caso
de terrenos rugosos, con cambios en orientaciones y pendientes, la suma vectorial
será pequeña y la dispersión elevada.
|
|
De acuerdo con Franklin (1987a:605), las estimaciones de la rugosidad
deben ser independientes de otros parámetros del relieve para reducir
la información redundante. Parece deseable, además, cierta
independencia de la escala del análisis, lo cual elimina algunas
aproximaciones excesivamente simples como las que usan el rango de altitud.
|
|
Una variante del método de Hobson es la siguiente:
|
1 |
Se calculan los vectores normales a los segmentos que conectan al punto problema
y sus vecinos más próximos. Para ello se calcula la pendiente
local  y se le asigna la
orientación que le corresponda f i
, predeterminada por la posición del punto. De acuerdo con
la notación utilizada anteriormente (página previa):
|
|
| |
(z1-z5)/1.414d |
(z2-z5)/d |
(z3-z5)/1.414d |
| Pendiente, g |
(z4-z5)/d |
… |
(z6-z5)/d |
| |
(z7-z5)/1.414d |
(z8-z5)/d |
(z9-z5)/1.414d |
| |
315º |
0º |
45º |
| Orientación, f |
270º |
… |
90º |
| |
225º |
180º |
135º |
|
2 |
A partir de los vectores resultantes, definidos por sus valores
(g , f ), se calculan
las coordenadas rectangulares del vector unitario normal a cada uno de ellos.
Las expresiones son (Upton y Fingleton, 1989:312):
|
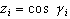
3 |
se calcula el módulo del vector suma de los vectores unitarios,
R :
 |
4 |
se calcula la varianza esférica,
 , como el complementario del
módulo medio  , que es el
módulo del vector suma normalizado al dividirlo por el número
de vectores unitarios (Band, 1989:286):
 |
|
La varianza esférica tendrá el valor cero para una rugosidad
nula —alineamiento completo de los vectores unitarios—y tenderá
a la unidad según se incrementa la rugosidad y, consecuentemente,
la dispersión de los vectores unitarios. |
|
|
MDR, modelo digital de
rugosidad
Modelo digital de rugosidad del valle de Degaña, construido
a partir de la desviación estándar de la pendiente. Las zonas
rugosas se representan en tonos claros y las lisas en tonos oscuros. |
 |
|
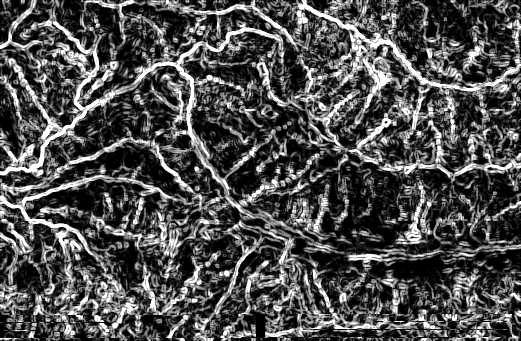
Este método de cálculo sobre las pendientes locales basado
en la varianza esférica de los vectores unitarios normales tiene la
ventaja de ofrecer estimaciones de la rugosidad independientes de la escala.
Al basarse en el módulo normalizado, los resultados son comparables
para cualquier tamaño de ventana que se use: 8 vecinos en una de 3x3,
24 en una de 5x5, etc. Esta normalización de la escala de medida permite
analizar adecuadamente las relaciones entre la rugosidad y la resolución
del modelo. |
|
|
|
|