Parte 6
La curvatura
La curvatura en un punto, h , puede definirse como la tasa de cambio en la pendiente y depende, por tanto, de las derivadas de segundo grado de la altitud —es decir, de los cambios de pendiente en el entorno del punto—.

Para el cálculo de la derivadas de segundo grado no es posible utilizar la aproximación simple empleada en la estimación de la pendiente y orientación, basada en un plano de ajuste. En este caso se utiliza una superficie de ajuste de segundo grado de acuerdo con la expresión general:

Para simplificar, representaremos el punto problema y sus vecinos con la notación que se muestra an la columna izquierda.
 

z1

z2

z3

z4

z5

z6

z7

z8

z9

En el caso concreto de la ventana de 3x3 centrada en el punto problema, los coeficientes de la ecuación cuadrática se calculan mediante las expresiones siguientes (Evans, 1979:29):

a00 = (2 (z2+z4+z6+z8)-(z1+z3+z7+z9)+5z5)/9
a10 = (z3+z6+z9-z1-z4-z7)/6d
a01 = (z1+z2+z3-z7-z8-z9)/6d
a11 = (z3+z7-z1-z9)/4d2
a20 = (z1+z3+z4+z6+z7+z9)/6d2 - (z2+z5+z8)/3d2
a02 = (z1+z2+z3+z7+z8+z9)/6d2 - (z4+z5+z6)/3d2
 

Se ha planteado la medida de la curvatura de tres formas distintas. La primera es la curvatura media, h, donde se mide la concavidad/convexidad general de la forma definida por el punto problema y sus 8 vecinos. Una expresión simple para el cálculo ha sido propuesta por Papo (1984:697), mediante la suma de las derivadas parciales de segundo orden con respecto a los ejes X e Y, de la forma siguiente:


 
Según el mismo autor, este método de estimación no es completamente exacto, ya que la curvatura depende de expresiones más complejas, pero presenta errores de pequeña magnitud para pendientes bajas y medias.

Las derivadas primeras de la expresión general son,

por tanto, las segundas:

y, sustituyendo obtenemos que


 
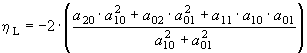
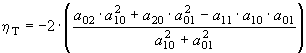
La curvatura media puede ser descompuesta en dos componentes ortogonales: la curvatura longitudinal hL —longitudinal convexity— que mide la concavidad/convexidad en el sentido de la máxima pendiente, y la curvatura transversal hT —cross-sectional convexity—, normal a la anterior. Wood (1996, Ap. 4.2.2) plantea las siguientes expresiones para su cálculo:

Puede observarse que sumando hL y hT se obtiene la misma expresión que para la curvatura general, . El signo negativo se debe a una convención que asume curvatura negativa cuando existe una concavidad y curvatura positiva en caso de formas convexas.
 
 

MDC, modelo digital de curvatura
Modelo digital de curvatura del valle de Degaña. Las zonas cóncavas se representan en blanco y las convexas en tonos oscuros.

    Modelo digital de curvatura
 
El problema de las expresiones de curvatura basadas en las líneas de pendiente es que pueden aparecer casos donde los coeficientes a10 y a01 son nulos aunque los otros no lo sean. Para prevenir esta circunstancia, Young (1978) propuso unas expresiones basadas en los otros coeficientes y que permiten conocer los valores de curvatura máxima y mínima independientemente de su dirección:

Las expresiones anteriores serán las más utilizadas para el reconocimiento de elementos morfológicos.