Parte 4
La pendiente
La pendiente en un punto del terreno se define como el ángulo existente entre el vector normal a la superficie en ese punto y la vertical. Es demostrable (Felicísimo, 1994:102, Wood, 1996, Ap. 4.2.1) que la pendiente g puede calcularse a partir de los componentes del gradiente mediante la expresión:

Dada la expresión del gradiente, el valor de g refleja la pendiente media en el entorno utilizado para calcular los componentes a10 y a01. La expresión anterior es la más utilizada en la práctica en el tratamiento de los modelos matriciales (Papo y Gelbman, 1984:698; Franklin, 1987a:604; Erdas, 1991:15) pero para el cálculo de la pendiente existe un buen número de alternativas cuyas ventajas y problemas deben evaluarse en cada caso y para cada aplicación.
 

MDP, modelo digital de pendientes
En la figura se muestra el modelo digital de pendientes de una zona del SO de Asturias. Las zonas planas se representan en tonos oscuros y las más inclinadas en tonos claros.

    Modelo digital de pendientes
 
Los métodos más habituales se clasifican en función del número de puntos que intervienen en el cálculo:
 
Con dos puntos:
  • pendiente máxima al vecino más próximo, para lo cual se calcula la pendiente local entre en punto problema y sus vecinos; es el algoritmo más rápido, no da una medida de la orientación y propone los valores de pendiente más elevados.
    Idrisi (Eastman, 1992:181) utiliza este método limitado a los 4 vecinos más próximos. MicroDEM lo utiliza con los 8 vecinos ponderando la distancia en diagonal —la luz de malla por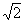

En este último caso:


 
Con tres puntos:
  • O’Neill y Mark (1987) proponen el uso del punto problema y de los vecinos Norte y Este para definir un plano. La pendiente de éste se asigna al punto problema. La selección de los vecinos mencionados es arbitraria y cambiarlos puede modificar el resultado tanto de la pendiente como de la orientación. La formulación sería equivalente a la expresión general, donde los componentes del gradiente son locales:


 
Con cuatro puntos:
  • utiliza los valores del gradiente calculados con los 4 vecinos más próximos, lo que equivale a estimar la pendiente del plano de ajuste a estos puntos. El punto problema no interviene en el cálculo.
     
Con ocho puntos:
  • Sharpnack y Akin (1988:248) proponen el operador de Prewitt para estimar la pendiente, con lo que los ocho vecinos tienen el mismo peso en el cálculo del gradiente. Es el método usado en Erdas™. El punto problema no tiene influencia en la pendiente.
  • Horn (1981) usa el operador de Sobel, que pondera más los 4 vecinos más próximos que los situados en las diagonales. Es el método usado en Arc/Info™ y el punto problema tampoco interviene en el cálculo.
     
El uso de cualquiera de los métodos anteriores debe valorarse en función del tipo de aplicación a desarrollar posteriormente. Los algoritmos basados en la pendiente local tienen a su favor que no introducen suavización en los datos como los basados en 4 y 8 puntos. El uso de sólo 4 vecinos no tiene justificación aparente y parece más adecuada la búsqueda de pendiente máxima con la totalidad de vecinos con control de la distancia en el caso de las diagonales. Los métodos basados en operadores de Prewitt y Sobel son menos sensibles al error en el MDE ya que, al intervenir un número elevado de puntos, las posibles desviaciones individuales pierden peso y pueden compensarse parcialmente entre ellas. En estos últimos, sin embargo, la altitud del punto problema no interviene en los datos por lo que la información del mismo se desaprovecha.