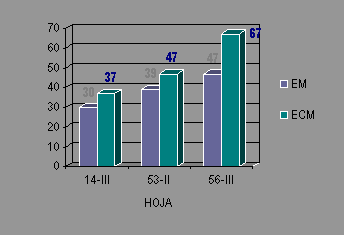
Diagrama de síntesis con los resultados del error en tres zonas de diferente relieve (ver texto)
El método de Monte Carlo
Los métodos de Monte Carlo son una potente herramienta de trabajo
cuando la solución analítica del problema es difícil.
El método implica:
A partir de los puntos anteriores es posible generar modelizaciones numéricas del proceso en número suficiente como para construir empíricamente la función de probabilidad de la variable resultado.
Los métodos de Monte Carlo han comenzado a ser prácticos y útiles cuando los ordenadores han estado disponibles de forma generalizada. Los generadores de números aleatorios son rutinas bien conocidas con las cuales es posible generar series de números cuyas distribuciones pueden ajustarse a múltiples modelos.
En el caso que se trata aquí, podemos asumir un error gaussiano o con cierto grado de autocorrelación. Los errores serán añadidos a datos simulados y aplicados los algoritmos que ejecutan la simulación. De los resultados podemos deducir las características de la propagación del error.
Felicísimo (1995) aplica este método al análisis de
la propagación del error altitudinal al cálculo de la pendiente.
Los pasos seguidos son los siguientes:
Obviamente, la pendiente esperada en ausencia de error es nula ya que el
MDE de partida muestra un terreno plano. Los resultados más notorios
son los siguientes:
| ECM | 5% |
10% |
20% |
| Error | 1,4º |
2,9º |
5,8º |
el ECM se establece en porcentaje del tamaño de la malla del MDE; por ejemplo, para un MDE de 30 m de intervalo entre datos, un ECM del 10% corresponde a 3 m
|
|
Diagrama de síntesis con los resultados del error en tres zonas de diferente relieve (ver texto) |