El error cartográfico: la deformación de los mapas

La deformación del mapa topográfico debido a cambios dimensionales provoca errores globales que afectan a la totalidad de los datos del modelo. Cuando los datos van a usarse en procesos de análisis y modelización es aconsejable realizar un estricto control de las dimensiones del problema desde el primer momento.

Cabe destacar que la detección y corrección de este tipo de errores sólo es posible cuando se trata de deformaciones globales. Esto significa que problemas tan usuales como los dobleces en los mapas pueden ser muy difíciles de corregir por tratarse de deformaciones locales.

La medida de este tipo de error puede realizarse con criterios estadísticos a partir de un conjunto de puntos de control localizados con precisión. El problema se plantea básicamente como una transformación de coordenadas, desde un sistema original deformado a otro de referencia, habitualmente un sistema de proyección geográfica.

Los programas de digitalización suelen tener incorporadas utilidades para realizar la corrección desde el principio pero también es posible realizarlo a posteriori mediante procesos de ajuste que la mayoría de los SIG poseen.

El método de corrección se ejecuta en tres pasos:

• se establece una serie de puntos de control cuya localización se conoce con exactitud en ambos sistemas de coordenadas
• se establecen unas funciones de transformación entre ambos sistemas, calculadas a partir de los puntos de control
• se aplican las funciones de transformación sobre los puntos de control para conocer la magnitud del error
• en caso de que el error sea aceptable, se realiza la transformación global aplicando las funciones a la totalidad de puntos

Las funciones de transformación suelen estimarse de forma independiente para las abscisas y para las ordenadas. Definiendo con el subíndice T a las coordenadas originales —tablero, por ejemplo— y con G a las finales —sistema de proyección—, se tienen las siguientes expresiones generales:

En la mayoría de los casos, las funciones anteriores se estiman aplicando métodos estadísticos de los cuales el más utilizado es el de superficies de tendencia, en el que las funciones z se calculan mediante regresión múltiple o ecuaciones polinómicas estimadas por el método de mínimos cuadrados. Se han propuesto funciones diferentes (Goshtasby, 1986, 1988) pero el método polinómico es el más utilizado. La expresión general del mismo es:

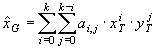
El grado del polinomio de ajuste puede ser variable. Cuando vale 1 es posible efectuar transformaciones afines, es decir, operaciones de translación, rotación y cambio de escala. Los grados superiores permiten recuperar distorsiones geométricas más complejas. En el primer caso, las ecuaciones de transformación se reducen a un plano de regresión:

.

La estimación del error cometido en la transformación: se realiza comparando las coordenadas de los puntos de control con las resultantes de aplicar las funciones de transformación sobre los mismos puntos. El error suele estimarse como error cuadrático medio, ECM, separable para las componentes x e y:

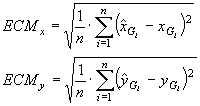
El límite aceptable para el error cuadrático máximo de los puntos o para el ECM debe fijarse en función de la aplicación a la que va destinado el MDE, así como de la escala de partida, primer determinante de la precisión geométrica de un modelo. En la digitalización manual puede proponerse un límite empírico que sería la distancia que corresponde a 0,25 mm del mapa a la escala de trabajo. Con un original a escala 1:50.000 este valor es de 12,5 m y corresponde aproximadamente a la precisión máxima que un operador experimentado puede obtener en la digitalización manual.

Esquema del proceso de corrección geométrica de los documentos digitalizados a partir de originales deformados.

En caso de errores excesivos deben examinarse individualmente los puntos de control para comprobar si existe alguno especialmente anómalo. Posteriormente, puede variarse el grado de la transformación para intentar mejores ajustes. De forma general, la transformación de primer grado sólo permite efectuar ajustes lineales por lo que, si el mapa está distorsionado, serán necesarias previsiblemente transformaciones de grado superior. Existe un límite práctico derivado de la precisión de los cálculos implicados en las operaciones matriciales necesarias.

Finalmente, debe destacarse que los puntos de control del mapa se digitalizan manualmente por lo que una introducción descuidada puede una causa complementaria de error muy significativa.