

Parte 16 |
|
la interpolación |
|
| Método general: IDW (ponderación
por distancia) |
|
| La interpolación del punto problema se realiza asignando pesos
a los datos del entorno en función inversa de la distancia que los
separa -inverse distance weighting, IDW-.
La fórmula general es:
donde |
|
|
Para establecer una función de proporcionalidad entre el peso y la distancia, la fórmula general queda como sigue:
|
| Esta familia de métodos permite la generación del MDE de
una forma rápida y simple. Sin embargo, se trata esencialmente de
una media ponderada y, por tanto, el resultado se encuentra siempre incluido
dentro del rango de variación de los datos. Por este motivo, el correcto
tratamiento de las formas cóncavas y convexas depende estrechamente
de la distribución de los puntos originales y la presencia de datos
auxiliares se hace muy conveniente. |
|
|
La hipótesis de la variable regionalizada
(kriging) |
| El kriging es un método de interpolación con una
expresión general similar a la anterior.
La diferencia básica es que asume que la altitud puede definirse como una variable regionalizada. Esta hipótesis supone que la variación espacial de la variable a representar puede ser explicada al menos parcialmente mediante funciones de correlación espacial: la variación espacial de los valores de z puede deducirse de los valores circundantes de acuerdo con unas funciones homogéneas en toda el área.
Las funciones pueden deducirse analizando la correlación espacial
entre los datos en función de la distancia entre ellos midiendo la
semivarianza entre datos separados por distancias
diferentes (Oliver y Webster, 1990:315, Royle et al., 1981). |
|
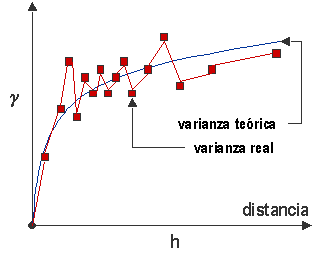
Ejemplo de semivariograma donde la varianza real se ajusta a una distribución teórica; ésta es la que se aplica para la estimación de los pesos en la interpolación. |
 |
Aunque el kriging es un método de estimación óptimo
desde el punto de vista estadístico, presenta algunas dificultades
a la hora de ser utilizado como método de construcción de los
MDE:
Por los motivos anteriores el kriging no suele dar buen resultado en la construcción de MDE, generándose modelos muy suavizados donde la rugosidad del terreno se infravalora fuertemente. |
|