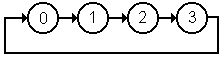3.5 SISTEMES SEQÜENCIALS
3.5.1 INTRODUCCIÓ A LA LÒGICA
SEQÜENCIAL.
Un sistema seqüencial és aquell en el qual la
sortida no sols està determinada pels valors instantanis de l'entrada,
sino que també ho està pel seu estat en un instan anterior.
Un exemple de sistema seqüencial és el que controla
la pujada o baixada d'un ascensor en un edifici. La seva entrada és
el pis al qual es vol anar i la sortida l'ordre de pujar o baixar. Eviedentment,
pujarem o baixarem segons quin sigui el pis on es troba l'ascensor. Aquest
és el seu estat.
Si E(t) és l'entrada , S(t) la sortida i Q(t) l'estat
d'un sistema seqüencial en un instant determinat t, la sortida i l'estat
en un instant posterior t+1 podran expressar-se com
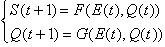
Els circuits combinacionals són un cas particular
en el qual la soritda depèn únicament dels valors instantanis
de les entrades:
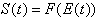
Sol ser habitual que la variable d'estat coincideixi amb
la variable de sortida.. Això és el que passa, per exemple,
amb els elements de memòria com són les bàscules biestables,
que són els que passarem a veure a continuació. Altres exemples
de sistemes seqüencials són els registres, els contadors,etc.
3.5.2 L'ELEMENT DE MEMÒRIA.
Una memòria és un sistema seqüencial que
conserva la informació que se li ha subministrat durant un temps
indefinit. La quantitat mínima d'informació que es pot ammagatemar
és un bit, y la memòria que fa aquesta funció és
la bàscula biestable o FLIP-FLOP.
Com el seu propi nom indica, és un sistema que té
dos estats estables. Això vol dir que no canvien excepte quan s'apliquen
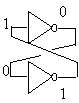
estímuls externs. El principi bàsic de funcionament es basa
en la utilitizació de dos inversors en oposició.
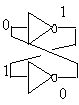
Amb la finalitat de disposar d'entrades que permetin provocar el canvi
d'estat, es substitueixen les portes NOT per portes NAND o NOR. Per exemple,
utilitzant portes NOR, tindriem l'anomenada bàscula S/R, que constitueix
l'element unitari de memòria.
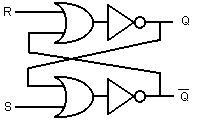
Aquest circuit manté el seu estat si les entrades estan inactives
(a 0), però si una de les dues s'activa, la sortida es posa a 0
o a 1, segons quina sigui l'entrada activada (amb un 1). A continuació
podem veure la seva taula de funcionament:
| R
|
S
|
Q+
|
| 0
|
0
|
Q-
|
| 1
|
0
|
1
|
| 0
|
1
|
0
|
Amb aquest circuit no hi ha cap possibilitat de control extern, com podria
ser un senyal de permís (habilitar o inhabilitar la bàscula)
o fer funcionar el circuit sincronitzat per un senyal de rellotge. Per
poder permetre aquesta possiblitat, cal complicar lleugerament el circuit.
La bàscula així obtinguda és la S-C o sincronitzada
per rellotge.
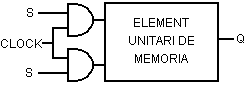
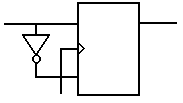
Normalment, un element de memòria es representa pel seu bloc.
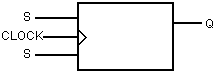
Un tipus de bàscula biestable d'especial interès per la seva
àmplia utilització en tot tipus de circuits d'electrònica
digital és la bàscula D o LATCH.
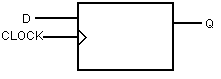
Bàsicament, aquesta bàscula està formada per una de
les anteriors, però amb les entrades connectades a D i a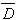 
respectivament. Es caracteriotza per treure per la sortida el que hi ha
a l'entrada cada cop que hi ha un pols de rellotge.
3.5.3 REGISTRES.
Reb el nom de registre un conjunt de bàscules biestables
destinades a uardar una certa informació binària (en general,
n bits) durant un cert periode de temps. Un cas d'especial interès
el constitueixen
els registres de desplaçament
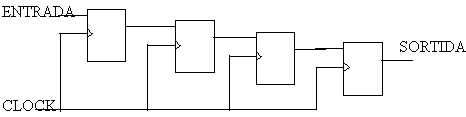
La informació a tractar entra per un extrem i va passant
d'un LATCH al següent fins arribar a la sortida, sincronitzat pel
rellotge
3.5.4 DISSENY GENERAL D'UN SISTEMA SEQÜENCIAL
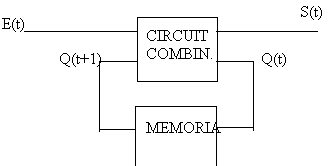
L'estructura general d'un sistema seqüencial és
la d'un sistema combinacional, però amb una realimentació
formada per una memòria que guarda l'estat anterior del sistema.
Per representar la manera de comportar-se d'un sistema seqüencial
disposem de diverses eines:
- Cronograma
- Taula d'estats.
- Diagrama d'estats.
El cronograma ens serveix per a concretar el comportament
de cadascuna de les variables i les seves relacions temporals amb les altres,
però no ens dona una idea clara de l'estat del sistema en un moment
determinat ni tampoc dona una visió clara del conjunt ja que només
ens mostra una de les possibles variacions que es poden produir en el circuit
en un moment determinat.
Pel que fa a la taula d'estats, ens relaciona les sortides
i els estats futurs en funció de les entrades i dels estats presents,
per a totes les combinacions possibles d'aquestes variables.
La representació de manera gràfica de tota
aquesta informació rep el nom de diagrama d'estats o graf d'estats.
En aquest graf, cada estat es representa mitjançant un cercle i
la transició entre estats mitjançant vectors que uneixen
els cercles. Aquest graf dóna una fàcil interpretació
del comportament del circuit i s'obté directament de la taula. Un
exemple de sistema seqüencial que podem representar d'aquesta manera
és un contador.
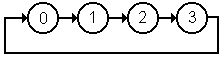
Un cop s'ha fet el disseny del sistema mitjançant
un diagrama d'estats, s'ha d'implementar físicament amb ajuda de
portes lògiques, blocs combinacionals i elements de memòria
3.5.5 EXERCICIS
