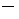 ) que cumpleixen
els següents postulats:
) que cumpleixen
els següents postulats:
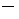 ) que cumpleixen
els següents postulats:
) que cumpleixen
els següents postulats:
| Postulat | ||
| clausura | els elements de B a+b
és un element de B |
els elements de B a*b
és un element de B |
| element neutre | ||
| commutativa | ||
| distributiva | ||
| complementari | 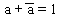
|
|
| El complementari d'un element és únic | ||
| Teorema | ||
| idempotència | ||
| principi de dualitat: | ||
| involució | 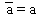 |
|
| absorció | ||
| associativa | ||
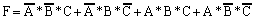 ; on
; on 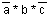 és
un terme (producte) canònic i els altres són termes.
és
un terme (producte) canònic i els altres són termes.
|
|
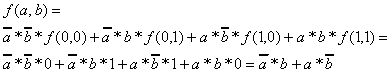
|


