Apunts 3.1

3.1 REPRESENTACIÓ DE LA INFORMACIÓ

Estudiarem un computador com una màquina que procesa informació en un sentit abstracte. Aquesta informació pot esser numèrica i no numèrica (texte, imatge, so, etc.), estudiarem a continuació quines són les tècniques més utilitzades per representar tot tipus d'informació.

3.1.1 VALORS ANALÒGICS I VALORS DISCRETS

Un senyal analògic pot prendre qualsevol valor, és equivalent als nombres reals. Per exemple el so, llum, la temperatura, etc.

Senyal Analògic
Un senyal discret pot prendre valors pertanyents a un conjunt acotat de valors, per exemple enters entre 0 i 4, les marxes d'un cotxe, les velocitats d'un ventilador, etc.

Senyal discret
Un senyal binari només pot prendre dos valors diferents. Per exemple un llum està encés o apagat, un tren està parat o en marxa, etc. Típicament s'asignen els valors '0' o '1' a les aquelles dues possibilitats; aquests valors corresponen, en general, a dos nivells elèctrics la magnitud dels quals depèn de la tecnologia.

Senyal binari
Exemple: Emmagatzamament i transmissió de veu mitjançant senyals binaris. Mitjançant tècniques de discretització i codificació podem representar un senyal analògic per senyals digitals (modulació per impulsos codificats)

Procés per codificar veu en binari:

3.1.2 CODIFICACIÓ

Codi :

És una representació biunívoca de la informació de forma que a cada informació diferent se li assigna una combinació de símbols determinada. Estudiarem sistemes de numeració on el valor de cada símbol també depen de la posició que ocupa, com el sistema de numeració decimal. El sistema de numeració romà no té un pes fixe associat a la posició, per exemple : el símbol V val 5, però el símbol I val 1 o -1 en funció de si va devant o al darrera de V, per aixó la aritmètica amb nombres romans no es possible, pesem com es farien les sumes.

SISTEMES I CODIS DE NUMERACIÓ: En un sistema de numeració, la base B indica el nombre de símbols que utilitza per la representació. El sistema decimal utilitza deu símbols diferents, 0 1 2 ... 9, i la base es B = 10. Els sistemes digitals actuen sobre variables que únicament poden adoptar dos estats diferents, per tant B = 2, i té dos símbols,normalment el 0 i el 1.

Representació d'un nombre: En un sistema en base B un nombre qualsevol N ( expressat en base 10) amb xifres : An An-1 ... A1 A0 A-1 ... A-p es pot representar amb un polinomi de potències de la base multiplicats pel símbol corresponent a la base. Aquest polinomi reb el nom de polinomi equivalent.

On:

Exemples: Quin valor representa el 425,4 en base 8 ?

Quin valor representa el 11010,01 en base 2 ?

* Sistema Binari:

O sistema de numeració en base dos. Utilitza com a símbols el 0 i 1. Cada digit rep el nom de BIT (Binary digIT). Així doncs, definim com a BIT la unitat míma d'informació comprensible per l'ordinador.

Podem utilitzar el pes de cadascuna de les posicions per a convertir sistemàticament un nombre binari a decimal. La posició n té un pes 2n.

Exemple:
16;8;4;2;1 10111₍₂ = 16+4+2+1 = 23

Binari			Decimal
Posició/Pes
2	1	0
2²	2¹	2⁰
4	2	1
0	0	0	0
0	0	1	1
0	1	0	2
0	1	1	3
1	0	0	4
1	0	1	5
1	1	0	6
1	1	1	7

Amb p bits podem representar 2^p nombres [0..2^p-1]. Això ens permet saber el nombre de bits (p) que necesitarem per representar el nombre decimal N.

Exemple: Volem representar magnituts fins al 10 ( N = 10), necessitarem: 2^p-1< N 2^p, per p = 4 resulta : 3 < 10 < 16, així dons són necessaris 4 bits.

Si volem representar el nombre 7 necessitem 3 bits:

2^3-1 <= 7 < 2³ => 3-1 < lg₂ 7 < 3

Si volem representar el nombre 8 necessitem 4 bits:

2^4-1 <= 8 < 2⁴ => 4-1 < lg₂ 8 < 4

La numeració binaria és molt útil per ser utilitzada per les máquines; no obstant, és bastant incómoda pels usuaris per necessitar moltes xifres per representar un nombre, per aquest motiu utilitzarem sistemes de numeració més condensats: l'octal i el hexadecimal.

* Sistema Octal:

Aquest sistema de numeració és un sistema posicional que utilitza 8 símbols (del 0 al 7) per representar les quantitats. La aritmética d'aquest sistema es semblant a la dels sistemas decimal i binari.

* Sistema Hexadecimal:

El Sistema Hexadecimal és un sistema de numeració en base 16. Necessita 16 símbols, de valor del 0 al 15, però els valors del 10 al 15 es representen normalment per 2 digits decimals, i aixó pot crear problemes de representació, per exemple si s'escriu 110₍₁₆ no sabrem si hi ha tres xifres 1 1 0, o dos 11 0, o també dos però 1 10, amb magnituds diferents. Per tant substituirem el 10 per A, 11 per B, etc. i ara 1 1 0 serà 110_(16, 11 0 serà B0₍₁₆, i 1 10 serà 1A₍₁₆

HEXADECIMAL	Símbol	0	1	2	...	A	B	C	D	E	F
DECIMAL	Valor	0	1	2	...	10	11	12	13	14	15

3.1.3 CANVIS DE BASE

N₍₁₀ --> A _(B . Per passar el nombre N expressat en el sistema decimal al sistema en base B utilitzarem el mètode de divisió- multiplicació:

Exemple: Passar el nombre 453,139₍₁₀ a base 8.

Part entera				Part fraccionària

Per tant 453,135₍₁₀ = 705,1071...₍₈

Nota: Cap xifra trobada pot ser igual o más gran que la base.

A_(B-->N₍₁₀. Per passar d'un sistema qualsevol al sistema decimal utilitzem el polinomi equivalent, ja que la expressió d'una magnitud queda, de manera natural, expresada en decimal.

Exemple: Convertir el nombre 705,11₍₈ a base 10.
7*8²+0*8¹+5*8⁰+1*8^-1+1*8^-2 = 7*64 + 0 + 5 + 0,125 + 0,015625 = 453,1406255

Per tant 705,11₍₈ = 453,1406255

A_(mⁿ -->C_(m. Per passar un nombre representat en base mⁿ a base n (bases relacionades mitjançant potències). Es passarà cadascun dels dígits a base m independentment utilitzant sempre n digits de la base n.

Exemple: De base 8 = 2³ a base 2, (m=2, n=3).
643,573₍₈= 110 100 011, 101 111 101₍₂

A_(m -->C _(mⁿ . Per passar un nombre representat en base m a base mⁿ. S'agrupen els bits d'n en n cap a la dreta i cap a l'esquerra de la coma i s'opera el polinomi equivalent de cada grup independentment.

Exemple: canviar de base 2 a base 16 el següent nombre: 110100011,101111101₍₂

Finalment, 110100011,101111101₍₂= 1A3,BE8 ₍₁₆

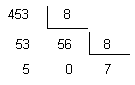
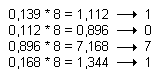
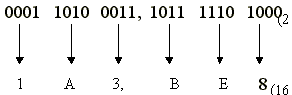
amb nombres enters.

amb nombres fraccionaris.

3.1.4 SUMA BINÀRIA

Abans d'estudiar la representació d'enters en binari, i amb l'objectiu d'oprar en arimètica binaria, repasarem l'aritmètica de la suma per analitzar el procés en detall.

Suma decimal (dues xifres):

Suma binària (dos bits):

La Taula de Veritat per la suma de dos bits és:

a	b	c	s
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Examinarem però un cas més general, suma de tres bits, en aritmètica binària:

Veurem ara totes les possibilitats d'aquest nou cas (suma binaria de tres bits).

c_n	a	b	c_n+1	s
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

3.1.5 REPRESENTACIÓ D'ENTERS EN BINARI

REPRESENTACIÓ DE ENTERS POSITIUS

Es representen directament pel seu codi binari, Per obtenir-los s'aplicarà un canvi de base, amb B = 2 pel mètode de la divisió.

Els nombres amb signe, positius i negatius, es poden representar de vàries formes. S'haura d'establir un mecanisme per fer un canvi de signe.

REPRESENTACIÓ DE ENTERS POSITIUS NEGATIUS.

1- Representació en Signe-Magnitut

És la mateixa representació que la que es fa servir pels nombres positius excepte la inclusió d'un bit (bit de signe) que indica si el nombre es positiu (0) o negatiu (1). Fer un canvi de signe serà simplement canviar el primer bit del codi.

El rang de representació amb n bits és

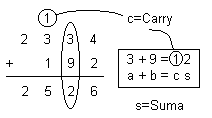
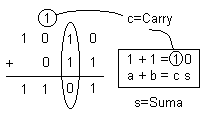
Exemple:

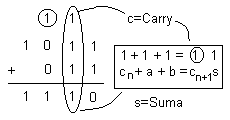
n = 3

3	0 1 1
2	0 1 0
1	0 0 1
0	0 0 0
-0	1 0 0
-1	1 0 1
-2	1 1 0
-3	1 1 1

Intentarem operar artimèticament amb el codi. Exemple 2 + 1.

	2	0	1	0
+	1	0	0	1
	------	------------	-------------	------------
	3	0	1	1

El resultat es correcte com era d'esperar amb un codi binari, provem ara una resta, 2-1=2+(-1).

	2	0	1	0
+	(-1)	1	0	1
	------	------------	-------------	------------
	1	1	1	1

El resultat es -3, i és incorrecte.

Inconvenients:

2- Representació en Complement A 1 (C1).

Els nombres positius es representen com en el cas de signe-magnitud. Per canviar de signe aplicarem el complement A1 de l' enter positiu de la mateixa magnitud. El complement a 1 d'un nombre s'obté substituint els 0's per 1's i viceversa.

El rang de representació amb n bits és

Propietat: C1(C1(A)) = A

Exemple:

3	0 1 1
2	0 1 0
1	0 0 1
0	0 0 0
-0	1 1 1
-1	1 1 0
-2	1 0 1
-3	1 0 0

Observació: En els nombres positius el primer bit és 0 i en els negatius és 1.

Intentarem operar artimèticament amb el codi. Exemple 3 - 1= 3 + (-1).

	3		0	1	1
+	(-1)		1	1	0
	------	------------	------------	-------------	------------
	2	(1)	0	0	1

El resultat es 1, incorrecte. S considerem el carry seria 9, també incorrecte.

Observacio: En els numeros positius el primer bit es 0 i en els negatius es 1.
Exemple: 18 = 00010010 i -18 = 11101101
Inconvenients:

3- Representació en Complement A 2 (C2)

Els nombres positius es representen com en el cas de signe-magnitud. Els negatius es representen com el complement A2, canvi de signe, del enter positiu de la mateixa magnitud. El complement A2 d'un nombre s'obté sumant 1 al séu complement A1: C2(A) = C1(A) + 1. Important: s'ignoraran els bits en excés, si el codi es de tres bits el resultat es de tres bits, si hi ha carry s'ignorarà.

El rang de representació amb n bits és

; i té la propietat: C2(C2(A)) = A

Exemple:

3	0 1 1
2	0 1 0
1	0 0 1
0	0 0 0
-1	1 1 1
-2	1 1 0
-3	1 0 1
-4	1 0 0

Observació: En els nombres positius el primer bit és 0 i en els negatius és 1.

Intentarem operar artimèticament amb el codi. Exemple 3 - 1= 3 + (-1).

		1	1	1
	3		0	1	1
+	(-1)		1	1	1
	------	------------	------------	-------------	------------
	2	(1)	0	1	0

El resultat es 2, correcte, positiu perque comença per 0. I l'operació 1 - 3 ?

			1
	1	0	0	1
+	(-3)	1	0	1
	------	------------	-------------	------------
	(-2)	1	1	0

Correcte també.

Exemple: 18 = 00010010 i -18 = C1(-18) + 1 = 11101101 + 1 = 11101110

4- Representació en Excés 2^-n (Sesgada)

Aquest métode de representació utilitza tots els bit per representar un valor. Aquest valor es correspon amb el nombre representat més l'excés, que per n bits correspon a 2^-n Així tot valor serà finalment positiu ja que el rang de valors representat és :

.

Exemple : per n = 8 el valor per excés es 128.

Si volem representar la magnitud 11, el codi resultant serà 11+128=139. Si fos el -11, el resultat seria -11+128= 117. El 139 i el 117 es codifiquen finalment amb una representació binaria d'enters positius

3.1.6 REPRESENTACIÓ DE NOMBRES FRACCIONARIS

Els nombres fraccionaris es poden representar en coma fixe i en coma flotant.

Coma fixa: La coma sempre està en una posició fixa. Dels n bits significatius, a bits representaran la part entera i n-a bits la part fraccionaria.

Part entera	Part Fraccionaria
a	n-a

Coma flotant: Qualsevol nombre es pot representar com

Mantissa B ^Exponent

La mantissa és un nombre representat en coma fixa i signe magnitud. Normalment la coma queda situada a l'esquerra de la primera xifra significativa (diferent de zero).

L'exponent és un nombre enter, en codificació excés 2^-n o sesgada. el signe queda incorporat sumant al valor original una quantitat constant.

El format binari empleat és⁴ n bits

Bit de signe	Exponent	Mantissa
1	n-a-1	a

Exemple (decimal): Representació de la magnitud decimal - 0.00000000056789 en coma flotant, diposarem de 8 digits decimals, (signe, 2 d'exponent i 5 de mantissa).

-0. 000 000 000 567 890 = - 5.6789 x 10^-10; Si utilitzem 50 com el valor constant esmentat, l'exponent seria 50-10 = 40. Així quedaria representat per 14056789 (), distribuït com:

1(-)

56789

En general el rang representat és (per la representació de l'exemple ):

3.1.7 ALTRES CODIS BINARIS

CODIS BCD: Són aquells que codifiquen directament cada dígit decimal en un codi binari.

Ponderats: En aquest cas els bits tenen un pes en funció de la posició que ocupen.

BCD NATURAL: Cada dígit es codifica en el codi binari de 4 bits. Els pesos són 8,4,2,1
BCD AIKEN: S'utilitza un codi de pesos 2,4,2,1

No ponderats: Els bits no tenen un pes associat.

BCD EXCÉS 3: Cada dígit N es codifica com el corresponent a N +3 en binari natural.

Decimal	BCD Natural	BCD Aiken	BCD excés 3
	8 4 2 1	2 4 2 1
0	0 0 0 0	0 0 0 0	0 0 1 1
1	0 0 0 1	0 0 0 1	0 1 0 0
2	0 0 1 0	0 0 1 0	0 1 0 1
3	0 0 1 1	0 0 1 1	0 1 1 0
4	0 1 0 0	0 1 0 0	0 1 1 1
5	0 1 0 1	1 0 1 1	1 0 0 0
6	0 1 1 0	1 1 0 0	1 0 0 1
7	0 1 1 1	1 1 0 1	1 0 1 0
8	1 0 0 0	1 1 1 0	1 0 1 1
9	1 0 0 1	1 1 1 1	1 1 0 0

CODI DE GRAY (Complementari).

És un codi contínu ja que les representacions de nombres decimals consecutius són adjacents (només difereixen en un bit) i és cíclic ja que la última és adjacent a la primera.

També rep el nom de reflexat, ja que per la formació de n bits es repeteix simètricament les seves combinacions afegint un 0 en les 2n-1 primeres i un 1 en les 2n-1 restants.

Decimal	Gray de 2 bits	Decimal	Gray de 3 bits
0	0 0	0	0 0 0
1	0 1	1	0 0 1
2	1 1	2	0 1 1
3	1 0	3	0 1 0
		4	1 1 0
		5	1 1 1
		6	1 0 1
		7	1 0 0

CODI DE JOHNSON (Complementari)

També reben el nom de progresius. Amb n bits pot codificar 2n nombres diferentes. Per codificar el nombre N és necesari un nombre de bits n tal que: 2(n-1)=<N<2n

Decimal	Jonhson de 3 bits bits	Decimal	Jonhson de 4 bits bits
0	0 0 0	0	0 0 0 0
1	0 0 1	1	0 0 0 1
2	0 1 1	2	0 0 1 1
3	1 1 1	3	0 1 1 1
4	1 1 0	4	1 1 1 1
5	1 0 0	5	1 1 1 0
		6	1 1 0 0
		7	1 0 0 0

3.1.8 REPRESENTACIÓ INTERNA DE DADES

Com s'ha comentat al inici de la secció, la informació que volem codificar no és sempre numèrica. Moltes vegades una computadora necessita emmagatzemar diversos tipus de caràcters.

* caràcters alfabètics

* xifres decimals: Del 0 al 9.
* caràcters especials

NUL Null (caràcter nul). CR Carriage return (retorn de carro). ACK Acknowledge (reconeixement de transmisió). FF Form feed (avanç de pàgina).LF Line feed (avanç de línea).

Ha estat definit com codi internacional l'ASCII. Consta de 127 símbols i per tant es necessiten 7 bits per codificar-los. Degut a que els ordinadors manipulen els bits de 8 en 8 (byte) el codi ASCII s'ha extès a 8 bits i d'aquesta manera es poden codificar símbols adicionals, com caracters nacionals, semigràfics o l'alfabet grec.

3.1.9 CODIS DETECTORS I CORRECTORS D'ERRORS

En la transmisió d'informació entre ordinadors a llarga o curta distancia, en las línies de transmisió, així com al codificar i decodificar la informació, apareixen errors que és necessari detectar i en alguns casos corretgir. Per això s'utilitzen una serie de códis detectors i correctors d'errors.

Definim distancia entre dues combinacions binaries com el nombre de bits que han de ser modificats en una de las combinacions per obtenir l'altra.

Definim distancia d'un códi com la menor de les distancies entre dues combinacions binaries qualsevols del mateix.

Per que un códi pugui detectar errors, la seva distancia ha de ser superior a la unitat, ja que si es 1, els errors d'un bit poden portar-nos a una altra combinació válida sense que poguem detectar-ho.

La distancia d'un códi està íntimament lligada al nombre d'errors capaç de detectar.

Un sistema senzill i molt utilitzat de detecció d'errors és la paritat. La paritat consisteix en afegir als codis originals un nou bit, anomenat de paritat, perquè el nombre d'1s del nou codi sigui sempre parell, ( també es podria acordar una quantitat senar de bits). Si hi ha un error, es canvia un 0 per 1 o vice-versa, el nombre d'1s del codi rebut no cumplirà la condició prevista i quedarà detectat. Si hi ha dos errors a la mateixa informació no es detecta amb aquest tipus de detecció d'errors.

Exemple :

Decimal	BCD excés 3 amb paritat senar
0	0 0 1 1 1
1	0 1 0 0 0
2	0 1 0 1 1
3	0 1 1 0 1
4	0 1 1 1 0
5	1 0 0 0 0
6	1 0 0 1 1
7	1 0 1 0 1
8	1 0 1 1 0
9	1 1 0 0 0

Els códis correctores, a més de detectar l'error el corretgeixen, però amb l'inconvenient de necessitar major nombre de bits que els anteriors. La distancia mínima que ha de tenir un códi per poder corretgir errors de 1 bit és 3. En general, per corretgir errors de n bits és necessari que la distancia del códi sigui al menys 2n+1.

3.1.10 UNITATS D' INFORMACIÓ EN INFORMÀTICA

Nom	Descripció
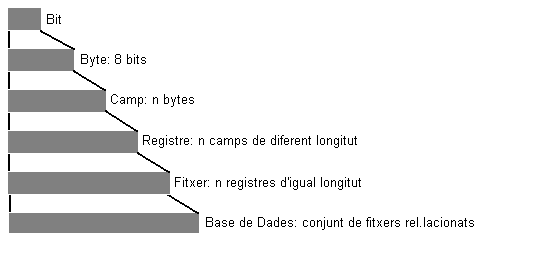
Bit	Mínima unitat d'informació, '0' o '1'.
Byte	Agrupació de 8 bits, de vegades se l'anomena caràcter, ja que pot contenir una lletra de text.
Camp	Unitat d'informació lògica d'una aplicació, per exemple nom, dni, ...
Registre	Conjunt de camps relacionats, en general té una estructura fixa. Per exemple : un client, un article, una assignatura, ...
Fitxer	Conjunt de registres d'idèntica estructura, relacionats de forma lògica: clients, articles, assignatures,...
Base de dades	Conjunt de fitxers relacionats

Valors Múltiples de byte:

Nom	Notació	Valor
Byte		8 bits
Kilobyte	Kb	1024 bytes = 2 ¹⁰ bytes
Megabyte	Mb	1024 kilobytes = 2 ²⁰ bytes
Gigabyte	Gb	1024 megabytes = 2 ³⁰ bytes
Terabyte	Tb	1024 gigabytes = 2 ⁴⁰ bytes