

|
DIBUJO ASISTIDO POR ORDENADOR TRANSFORMACIONES 2D |
Una de las mayores virtudes de los graacute;ficos generados por ordenador es la facilidad con se pueden realizar algunas modificaciones sobre las imágenes. Un gerente puede cambiar la escalas de las gráficas de un informe. Un arquitecto puede ver un edificio desde distintos puntos de vista. Un cartógrafo puede cambiar la escala de un mapa. Un animador puede modificar la posición de un personaje. Estos cambios son fáciles de realizar porque la imagen gráfica ha sido codificada en forma de números y almacenada en el interior del ordenador. Los números son susceptibles a las operaciones matemáticas denominadas transformaciones.
Las transformaciones nos permiten alterar de una forma uniforme toda la imagen. Es un hecho que a veces es maacute;s fácil modificar toda la imagen que una porción de ella. Esto supone un complemento muy útil para las técnicas de dibujo manual, donde es normalmente más fácil modificar una pequeña porción del dibujo que crear un dibujo completamente nuevo.
Es este capiacute;tulo veremos transformaciones geométricas como el cambio de escala, la traslación y la rotación. Veremos como se expresan de una forma sencilla mediante multiplicaciones de matrices. Introduciremos las coordenadas homogéneas con el fin de tratar de una manera uniforme las transformaciones y como anticipo de las transformaciones producidas por la perspectiva en los modelos tridimensionales.
Las imaacute;genes gráficas que hemos generado están compuestas por un conjunto de segmentos que están representados por las coordenadas de sus extremos. Algunos cambios en la imagen pueden ser fácilmente realizados mediante la aplicación de algunas operaciones matemáticas sobre estas coordenadas. Antes de ver algunas de las posibles transformaciones, repasemos algunas de las herramientas matemáticas que vamos a necesitar, como la multiplicación de matrices.
Para nuestro propoacute;sito, consideremos que una matriz es un conjunto bidimensional de números, por ejemplo:

son cuatro matrices diferentes.
Supongamos que definimos la matriz A como:
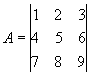
Entonces el elemento situado en la segundo fila y la tercera columna seraacute; ![]() y tendrá un valor de 6.
y tendrá un valor de 6.
La operacioacute;n matricial que más emplearemos será la multiplicación de matrices. La multiplicación de matrices es algo más complicada que la simple multiplicación de dos números; supone varios productos sencillos y sumas de los elementos de la matriz. No todas las parejas de matrices pueden ser multiplicadas. Se pueden multiplicar dos matrices A y B si el número de columnas de la primera matriz A es igual al número de filas de la segunda matriz B. Por ejemplo, si escogemos como matriz A la última que hemos visto y como matriz B la siguiente:
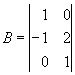
entonces podemos multiplicar A por B porque la primera tiene tres columnas y la segunda tres filas. Al contrario que la multiplicacioacute;n de números, la multiplicación de matrices no es conmutativa, es decir, aunque podemos multiplicar A> por B no podemos multiplicar B por A, por que B tiene sólo dos columnas que no se corresponden con las tres filas de A. Cuando multiplicamos dos matrices se obtiene como resultado otra matriz. Esta matriz producto tendrá el mismo número de filas que la primera de las matrices que se multiplican y el mismo número de columnas que la segunda. La multiplicación de la matriz ![]() A con la matriz
A con la matriz ![]() B da como resultado la matriz
B da como resultado la matriz ![]() C.
C.
Los elementos de la matriz producto C se expresan en funcioacute;n de los elementos de las matrices A por B mediante la siguiente fórmula:
![]()
En nuestro caso particular de ![]()
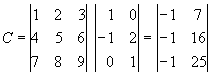
La multiplicacioacute;n de matrices es una operación asociativa. Esto significa que si tenemos varias matrices para multiplicar a la vez, no importa cuales multipliquemos primero. De forma matemática:
![]()
Esta es una propiedad muy uacute;til; nos permitirá combinas varias transformaciones gráficas en una sola transformación, produciendo como resultado unos cálculos más eficientes.
Existe un conjunto de matrices que cuando multiplican a otra matriz, la reproducen. Por esta razoacute;n reciben el nombre de matrices identidad. Son matrices cuadradas (tienen el mismo número de columnas y de filas) con todos los elementos 0 excepto los elementos de la diagonal principal, que valen todos 1. Por ejemplo
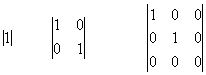
De forma matemática:
![]()
¿Coacute;mo se aplica todo esto a los gráficos? Bueno, consideremos un punto P1=[x1 y1] como una matriz ![]() . Si la multiplicamos por una matriz
. Si la multiplicamos por una matriz ![]() T , obtendremos otra matriz
T , obtendremos otra matriz ![]() que puede ser interpretada como otro punto.
que puede ser interpretada como otro punto.
![]()
Por tanto, la matriz T es una aplicacioacute;n entre el punto original P1 y el nuevo punto P2. Si suponemos nuestra imagen compuesta por los vértices de un polígono. ¿Qué pasará si transformamos cada uno de los punto mediante una multiplicación por una matriz T y dibujamos el resultado? ¿Qué aspecto tendrá esta nueva imagen? La respuesta, por supuesto, depende de los elementos de la matriz T. Si, por ejemplo, escogemos la matriz identidad entonces la imagen no se verá alterada.
Sin embargo, si escogemos la matriz
![]()
entonces
![]()
Cada una de las nuevas coordenadas x tiene el doble de valor que las antiguas. Las liacute;neas horizontales serán dos veces más largas en la nueva imagen. La nueva imagen tendrá la misma altura, pero parecerá que la hemos estirado hasta alcanzar el doble del ancho original.
|
antes |
después |
En general, las transformaciones de la forma
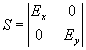
cambian el tamaño y la proporción de la imagen. Se denominan transformaciones de escalado. Ex es el factor de escala para la coordenada x y Ey es de la coordenada y.
|
antes |
después |
La siguiente transformación gráfica que vamos a ver es la rotación. Para introducir esta transformación recordaremos brevemente algunos conceptos trigonométricos. Sea un punto p1=(x1, y1) y lo giramos alrededor del origen un ángulo q para pasar a una nueva posición p2=(x2, y2). Queremos encontrar la transformación que convierte (x1, y1) en (x2, y2). Pero, antes de comprobar si alguna transformación es la adecuada, debemos saber primero que (x2, y2) debe escribirse en función de (x1, y1) y q. Para esto es necesario recordar la razones trigonométricas de seno y coseno.
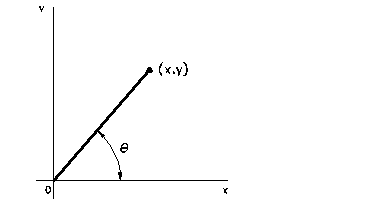
Definición de ángulo
A la vista de esta figura sabemos que
![]()
Es importante señalar que cuando la longitud del segmento es la unidad
![]()
También emplearemos las siguientes relaciones trigonométricas para determinar como gira un punto:

Ahora estamos listo ya para determinar la rotación de un punto alrededor del origen.
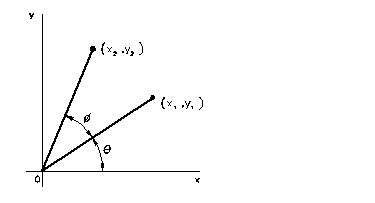
Rotación de un punto alrededor del origen
A la vista de esta figura tenemos:
![]()
donde L es la distancia del punto al origen de coordenadas. Por otro lado:
![]()
que nos lleva a
![]()
De forma análoga:
![]()
dando
![]()
A la vista de estas ecuaciones podemos imaginar una matriz que relacione las coordenadas del punto original y del punto girado:
![]()
Asiacute; la matriz de transformación para una rotación en sentido contrario a las agujas del reloj de ángulo f alrededor del origen es
![]()
Para una rotación en el sentido de las agujas del reloj, basta sustituir en la expresión anterior el valor del ángulo por -f. Así nos queda
![]()
COORDENADAS HOMOGÉNEAS Y TRASLACIÓN
Supongamos que necesitamos realizar un giro alrededor de un punto que no es el origen. Si fuésemos capaces de trasladar toda la imagen de un punto a otro de la pantalla, podríamos realizar este giro moviendo primero la imagen hasta que el centro de rotación coincida con el origen, luego realizamos la rotación y, por último, devolvemos la imagen a su posición original.
Desplazar la imagen recibe el nombre de traslación. Se realiza de una forma sencilla mediante la suma a cada punto de la cantidad que vamos a mover la imagen.
En general, con el fin de trasladar un imagen (Tx, Ty), cada punto (x1, y1) se convierte en uno nuevo (x2, y2) donde
![]()
Desafortunadamente, esta forma de describir la traslación no hace uso de matrices, por lo tanto no podría ser combinada con las otras transformaciones mediante una simple multiplicación de matrices. Tal combinación sería deseable; por ejemplo, hemos visto que la rotación alrededor de un punto que no sea el origen puede realizarse mediante una traslación, una rotación u otra traslación. Sería deseable combinar estas tres transformaciones en una sola transformación por motivos de eficacia y elegancia. Una forma de hacer esto es emplear matrices ![]() en vez de matrices
en vez de matrices ![]() , introduciendo una coordenada auxiliar w. Este método recibe el nombre de coordenadas homogéneas. En estas coordenadas, los puntos están definidos por tres coordenadas y no por dos. Así un punto (x, y) estará representado por la tripleta (xw, yw, w). Las coordenadas x e y se pueden recuperar fácilmente dividiendo los dos primeros números por el tercero respectivamente. No emplearemos la coordenada w hasta que no veamos las transformaciones tridimensionales de perspectiva. En dos dimensiones su valor suele ser 1 para simplificar. Sin embargo, lo veremos de forma general como anticipo de las transformaciones tridimensionales.
, introduciendo una coordenada auxiliar w. Este método recibe el nombre de coordenadas homogéneas. En estas coordenadas, los puntos están definidos por tres coordenadas y no por dos. Así un punto (x, y) estará representado por la tripleta (xw, yw, w). Las coordenadas x e y se pueden recuperar fácilmente dividiendo los dos primeros números por el tercero respectivamente. No emplearemos la coordenada w hasta que no veamos las transformaciones tridimensionales de perspectiva. En dos dimensiones su valor suele ser 1 para simplificar. Sin embargo, lo veremos de forma general como anticipo de las transformaciones tridimensionales.
En coordenadas homogéneas la matriz de cambio de escala
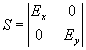
se convierte en
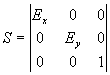
Si aplicamos esta matriz a un punto (xw, yw, w) obtenemos
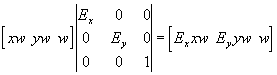
Si dividimos ahora por el tercer valor w tenemos (Exx, Eyy) que es el punto correcto cambiado de escala. En el caso de la matriz de rotación en sentido antihorario
![]()
se convierte, usando coordenadas homogéneas, en:
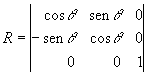
Si aplicamos esta matriz a un punto (xw, yw, w) obtenemos
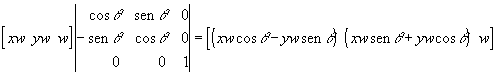
para dar el punto correctamente rotado
![]()
La matriz de transformación para una traslación Tx, Ty en coordenadas homogéneas es
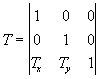
Para comprobar que esto es así apliquemos la matriz a un punto genérico
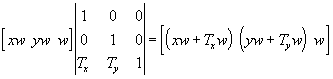
que nos da el punto trasladado ![]() .
.
ROTACIÓN ALREDEDOR DE UN PUNTO CUALQUIERA
Determinemos ahora la matriz de transformacioacute;n para la rotación en sentdio antihorario alrededor del punto (xC, yC).
Haremos esta transformación en tres pasos. Primero trasladaremos el punto (xC, yC) al origen, luego haremos la rotación alrededor del origen y, por último, devolveremos el centro de rotación a su posición original.
La traslación que desplaza al punto (xC, yC) al origen es

la rotación es
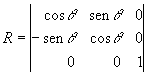
y la traslación que devuelve al centro de rotación a su posición es
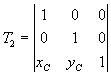
Para transformar un punto podemos realizar la siguiente multiplicación
![]()
pero, teniendo en cuenta la propiedad asociativa de la multiplicación de matrices, podemos multiplicar todas las transformaciones primero para obtener la matriz global de transformación
![]()
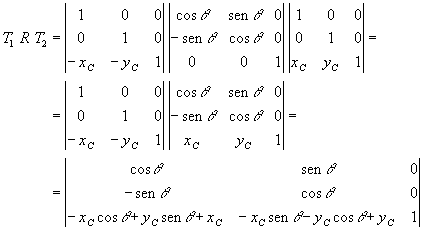
Cabe destacar que esta matriz se puede formar también mediante una rotación inicial de ángulo q y una traslación definida por los valores contenidos en la tercera fila.
Las tres transformaciones de cambio de escala, rotación y traslación son las más útiles y las más usadas. Son también posibles otras transformaciones. Dado que una matriz
![]() cualquiera
cualquiera
![]()
puede convertirse en una matriz ![]() en coordenadas homogéneas como
en coordenadas homogéneas como

sólo presentaremos algunas de estas transformaciones como matrices ![]() :
:
|
|
reflexión respecto al eje y |
|
|
reflexión respecto al eje x |
|
|
reflexión respecto al origen |
|
|
reflexión respecto a la recta y=x |
|
|
reflexión respecto a la recta y=-x |
|
|
deformación en el eje y |
|
|
deformación en el eje x |
Las primeras tres reflexiones son simples cambios de escala pero con factores negativos. Las simetrías respecto a las rectas y=x e y=-x pueden realizarse mediante un cambio de escale y un giro posterior. Es posible realizar las deformaciones mediante una secuencia de rotaciones y cambios de escala, aunque es mucho más fácil aplicar construir la matriz resultante. De igual forma se pueden construir transformaciones de cambio de escala y rotación a partir de las deformaciones.