DIBUJO ASISTIDO POR ORDENADOR RECTAS PERPENDICULARES

Construcción para comprobar si dos rectas son perpendiculares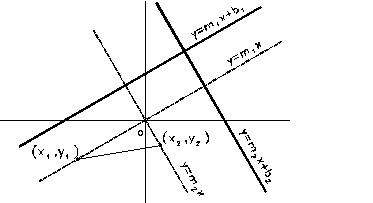

Tomemos ahora un punto (x₁, y₁) de , que verifica ; y un punto (x₂, y₂) de , que cumple . Los puntos (x₁, y₁), (x₂, y₂) y el origen forman un triángulo. Si las dos rectas son perpendiculares, el triángulo será recto y se cumplirá el teorema de Pitágoras:

Simplificando la expresión anterior, se obtiene:

o

pero, como e , tenemos:

Por lo tanto, dos rectas son perpendiculares, cuando la pendiente de una es la inversa de la otra cambiada de signo.

VECTORES

¿Qué es un vector? Un vector tiene una dirección única y un módulo. Un vector puede representarse por el par donde D_x es el desplazamiento a lo largo del eje x y D_y es el desplazamiento a lo largo del eje y.

Al contrario que los segmentos, los vectores no tienen una posición fija en el espacio. Nos indican cuanto y en que dirección nos tenemos que mover, pero no nos indican donde tenemos que empezar. La idea del vector es útil porque refleja aproximadamente el comportamiento de un lápiz que dibuja líneas sobre un papel o un rayo de electrones dibuja líneas sobre una pantalla de rayos catódicos.

PIXELS

¿Cómo se refleja todo esto en una pantalla gráfica? Para empezar, la noción matemática de un infinito número de puntos infinitesimales no es aplicable en una pantalla gráfica. No podemos representar un número infinito de puntos en un ordenador, así como tampoco podemos representar una cantidad infinita de números. Las máquinas son finitas, y estamos limitados a un número finito de puntos que componen cada una de las líneas de la pantalla, cuyo número varía desde varios cientos a varios miles. El máximo número de puntos distinguibles que una línea puede tener es una medida de la resolución de la pantalla. Cuanto mayor es el número de puntos mayor es la resolución. Esta limitación en el número de puntos no debe preocuparnos mucho, ya que el ojo humano no aprecia detalles más allá de los 1000 puntos por segmento. Ya que hemos de construir nuestras líneas a partir de un número finito de puntos, cada uno debe tener un cierto tamaño y no será por tanto un punto de verdad. Recibe el nombre de pixel (de las palabras inglesas picture element). Un pixel es el elemento direccionable más pequeño de la pantalla. Es la porción más pequeña que podemos controlar. Todos los pixel tienen un nombre o una dirección. Los nombres que identifican a los pixel corresponden a las coordenadas que definen a los puntos. Esto es parecido a la forma de seleccionar los elementos de una matriz mediante subíndices. Las imágenes gráficas creadas por ordenador se obtienen activando la intensidad y el color de los pixel que componen la pantalla. Se dibujan segmentos iluminando, es decir, dando brillo a un conjunto de pixel situados entre el pixel inicial y el pixel final. Podemos pensar en la pantalla como una malla o matriz de pixel. Debemos dar coordenadas enteras a cada uno de ellos. Empezando a la izquierda con 1, se numera cada una de las columnas. Empezando abajo con 1, se numera cada una de las filas. Las coordenadas (i, j) de un pixel indican por tanto la columna y la fila en la que está situado.

Ejemplo de pixel iluminado

Se colocan los valores de intensidad de todos los pixel en una matriz en la memoria del ordenador. De esta forma la pantalla gráfica puede acceder a esta matriz para determinar la intensidad con la que debe iluminarse cada pixel. Esta matriz, que contiene una representación interna de la imagen, se denomina frame buffer.

El proceso de activación de los pixel para un determinado segmento se denomina generación de un vector. Si conocemos los extremos que definen al segmento, ¿cómo decidimos que pixel deben ser activados? Existen varios esquemas para seleccionar estos pixel. El método que presentamos aquí recibe el nombre de Analizador Diferencial Digital Simétrico (ADD). Este nombre se deriva de la utilización de un método numérico similar al empleado para la resolución de ecuaciones diferenciales. Sin embargo, la ecuación diferencial que vamos a resolver es una muy sencilla, la que corresponde a una línea recta, y en vez de imprimir la solución, la vamos a dibujar.

Empezaremos por considerar otra forma de la ecuación de una recta. La denominada forma paramétrica porque damos los valores de x e y en función de un parámetro u. Supongamos que queremos representar el segmento comprendido entre los puntos (x₁, y₁) y (x₂, y₂). Queremos que la coordenada x varíe uniformemente entre x₁ y x₂. Esto podría representarse mediante la ecuación:

Cuando u vale 0, x vale x₁. A medida que u crece hasta 1, x se mueve uniformemente hacia x₁. Pero un segmento de recta, necesitamos que la coordenada y varíe también entre y₁ e y₂ de manera uniforme, al mismo tiempo que cambia x.

Estas dos ecuaciones en conjunto describen una línea recta. Esto se demuestra despejando el parámetro u en ambas ecuaciones e igualando las expresiones que se obtienen. Estas ecuaciones sugieren un método para seleccionar los pixel que deben ser iluminados. La idea es empezar dando a u el valor 0 e ir aumentándolo en pequeñas pasos hasta alcanzar el valor 1. A medida que hacemos esto, x e y se desplazan a lo largo del segmento de recta en pequeños pasos. Este es el tipo de algoritmo que es útil para dibujar una línea. En cada paso iluminamos el pixel que contiene el punto (x, y).

GENERACIÓN DE CURVAS

Hasta ahora hemos trabajo con segmentos rectos. Ya vimos como estos segmentos son fáciles de generar. Luego aprendimos como representar y manipular estos segmentos. Las líneas rectas tienen una representación matemática sencilla, que las hace muy fáciles de manejar en operaciones como las transformaciones y el recorte. Sin embargo, el mundo real no está compuesto únicamente por figuras lineales. Muchas de las cosas que podríamos querer modelar y dibujar supone la utilización de curvas.

Existen dos planteamientos para la representación de curvas. Uno es desarrollar un algoritmo de generación de curvas como el ADD antes. Con este planteamiento se crea una curva real. El segundo método es aproximar la curva mediante un determinado número de pequeños segmentos rectos. Las técnicas de interpolación que veremos más adelante se emplean en este segundo planteamiento. Empezaremos considerando la generación de curvas reales.

Supongamos que tenemos una curva, tal como un arco de circunferencia, que queremos dibujar. Si conocemos la ecuación diferencial de esta curva, podemos escribir un algoritmo Analizador Diferencial Digital Simétrico que nos permitirá calcular las coordenadas de los puntos de la curva.

Las ecuaciones diferenciales para curvas sencillas tales como círculos y elipses son bastante fáciles de resolver, y los algoritmos para su generación se pueden implementar directamente en el hardware. Así un dispositivo gráfico puede ser capaz de dibujar tanto líneas rectas como arcos.

Veamos un ejemplo, con la creación paso a paso de un algoritmo para la creación de arcos de circunferencia. Las ecuaciones del arco se pueden escribir en función del ángulo a como sigue:

donde es el centro del arco y R es el radio.

Si derivamos las expresiones anteriores tenemos

De esta forma podemos saber las cantidades que hay que añadir a las coordenadas de un punto viejo para obtener un punto nuevo.

Estas ecuaciones constituyen el núcleo del algoritmo de generación de arcos. El valor del incremento angular en cada paso debe ser lo suficientemente pequeño para que no haya huecos entre los pixel que definen la curva y de una buena aproximación del arco.

Existen, sin embargo, algunos problemas que surgen cuando se generan curvas a esta nivel. Para definir una curva, necesitamos más información que sólo sus extremos. También puede surgir otro problema cuando se apliquen transformaciones. Un segmento recto sigue siendo recto cuando cambia su escala, pero otros curvas podrían comportarse de forma distinta. Por ejemplo, cuando cambiamos la escala de una circunferencia sólo en una dirección se convierte en una elipse. Si únicamente tenemos un generador de arcos de circunferencia, estaremos muy limitados a la hora de escalar nuestras imágenes. Otro problema surge de la necesidad de recortar las curvas cuando se salen del área de dibujo. Aunque todos estos inconvenientes no son desdeñables queda todavía un último problema: no todas las curvas que queramos dibujar tendrán un algoritmo de generación sencillo. Las curvas que se emplean en la representación de las alas de un avión o los alerones de los coches de carreras o las caras humanas no son simples arcos y elipses. Tendremos que aproximar tales curvas mediante trozos de arcos de circunferencia, elipses y espirales. Pero podríamos también juntar muchos segmentos rectos a los que luego sería posible aplicar las transformaciones y algoritmos que veamos aquí.

Índice