|
|
DIBUJO ASISTIDO POR ORDENADOR POLÍGONOS INTERPOLANTES |
Los lados de un polígono pueden ser redondeados también mediante la utilización de las funciones de curvatura que hemos visto anteriormente. De hecho, un polígono es mucho más fácil de manejar, ya que no es necesario procesar por separado las regiones inicial y final. Lo único que hacemos es avanzar alrededor del polígono, suavizando cada uno de los lados mediante varios segmentos pequeños. Se empieza con un polígono que tiene unos pocos lados y se termina un nuevo polígono que tiene muchos más lados y aparece más redondeado.
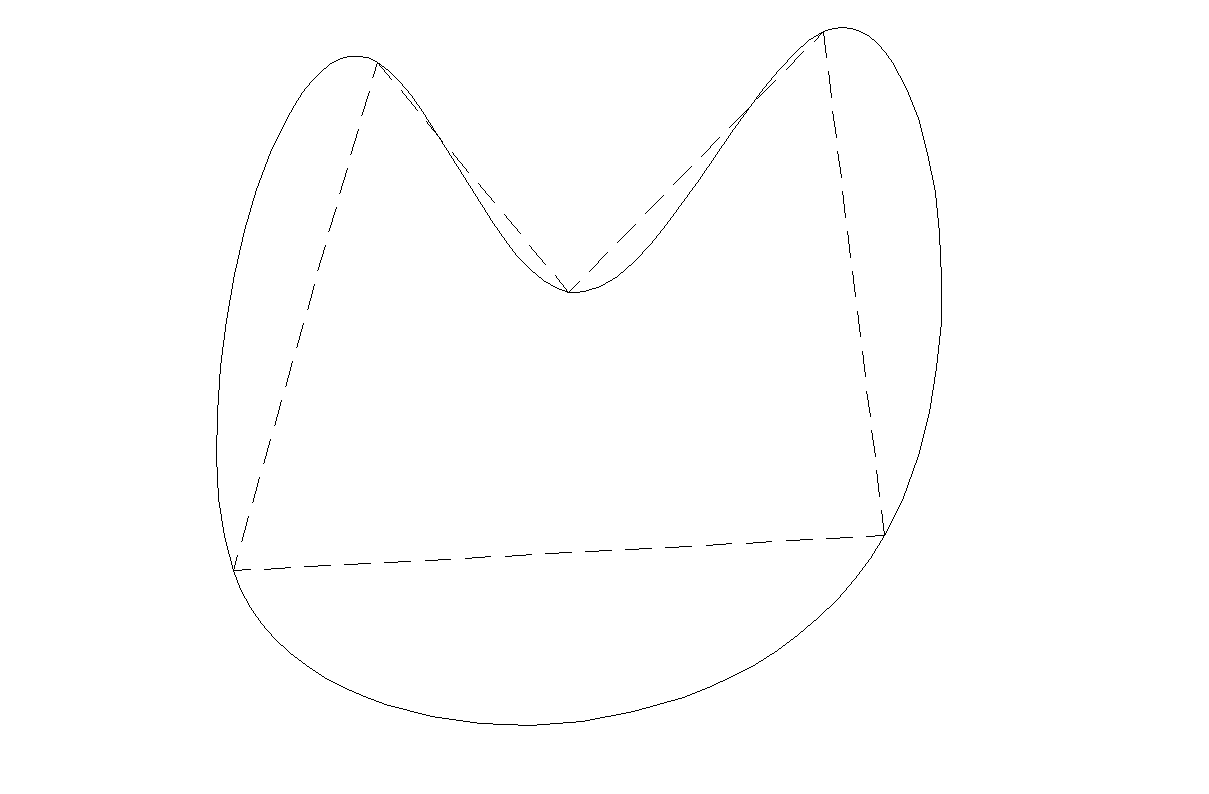
Suavizado de un polígono
Ahora que hemos presentado un método de interpolación utilizando nuestras funciones de curvatura caseras, examinemos sus inconvenientes. Algo que debemos tener en cuenta es que la suma de las funciones de curvatura no es 1 para todos los valores de u. Las funciones de curvatura han sido diseñadas para sumar 1 cuando el parámetro tiene un valor entero, pero no en las regiones intermedias. ¿Qué significa esto? Supongamos que
todos los puntos de referencia tienen la misma coordenada x, 
. Queremos, entonces, que las curva aproximada tenga también un valor constante de x en los puntos intermedios, pero la curva aproximada es
que para 
da
Sólo conseguiremos este efecto si la suma de las funciones de curvatura es 1 para todos los valores de u. Este inconveniente supone también que las curvas que deberían estar contenidas en un plano pasan de un lado a otro del mismo. Este problema podría resolverse normalizando las funciones, es decir, dividimos los valores obtenidos por la suma de todos ellos para cada valor de u.
Pero, este no es el único problema. Cada una de las secciones de la curva está conectada con la siguiente en un único punto de control, pero la pendiente en este punto podría no coincidir en las dos secciones. Esto significa que podrían existir esquinas en los puntos de control y no tendríamos por tanto una curva completamente suavizada.
Por último, al obligar a la curva que pase por cada uno de los puntos de control, reducimos hasta anularlo el efecto de los restantes puntos de referencia; pero a medida que nos alejamos del punto, todos los puntos que están en la misma región adquieren un cierto control sobre la curva. De esta forma, vemos como el control de la curva por un determinado punto de referencia sube y baja a medida que varía u.
Un comportamiento más natural sería que cada punto de referencia variase su control sobre la curva desde cero, cuando estamos muy alejados de él, hasta alcanzar el máximo, cuando nos acercamos a él. Podemos conseguir esto si no obligamos a la curva a pasar por los puntos de control, sino que tiramos de ella hacia la vecindad de cada punto. El resultado será una curva que sigue los contornos generales indicados por los puntos de referencia pero que no pasa en realidad por ninguno de ellos. Un conjunto de funciones de curvatura que siguen este planteamiento y también suman siempre 1 reciben el nombre de B splines.
La obtención de estas funciones está más allá del objetivo de estos apuntes, pero presentaremos e implementaremos las funciones B splines cúbicas, que son adecuadas para la mayoría de las aplicaciones. Estas funciones interpolan a partir de cuatro puntos de referencia y son polinomios de grado 3 en u, tal como nuestras funciones caseras. Las funciones B splines cúbicas para la zona intermedia de la curva son:
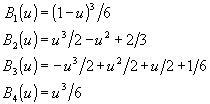
Para empezar o terminar una curva aproximada con B splines cúbicas son necesarias dos secciones especiales. Las siguientes expresiones se deben emplear para aproximar la primera sección de la curva
La última porción de la curva necesita
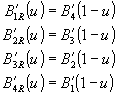
La segunda sección de la curva también tiene sus propias funciones de curvatura
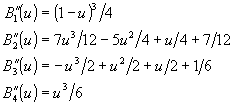
Y la penúltima sección de la curva emplea la inversa de estas funciones
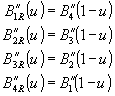
Suavizado mediante B splines
Las curvas B splines también se pueden emplear para suavizar polígonos.
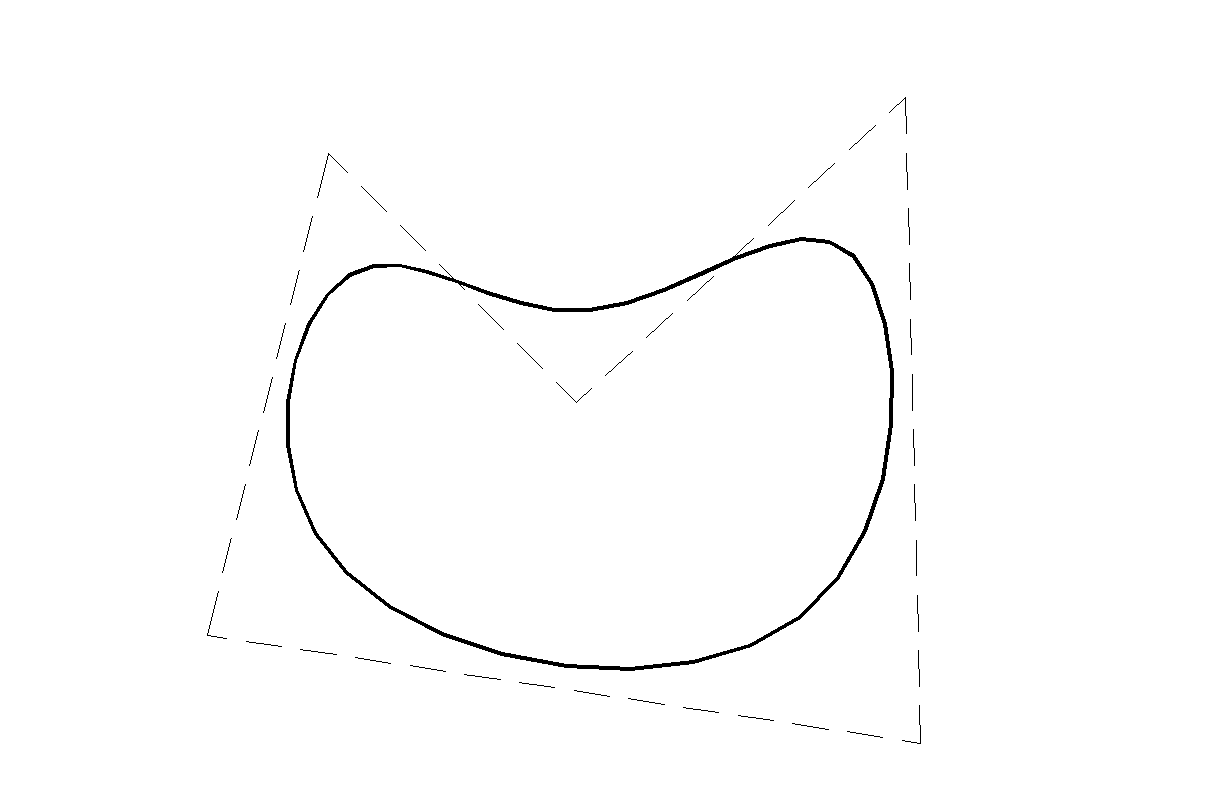
Suavizado de un polígono mediante curvas de B splines cúbicas
Las curvas B splines fueron diseñadas para eliminar las esquinas agudas en las curvas y, por otro lado, la curva tampoco pasa por los puntos de referencia. Sin embargo, también se pueden producir esquinas agudas y obligar a pasar la curva por los puntos de control mediante B splines, si es necesario. Esto se consigue usando varios puntos de control idénticos.
Cuando se emplean dos puntos idénticos la curva se acerca más a ese punto y la esquina se hace más aguda.
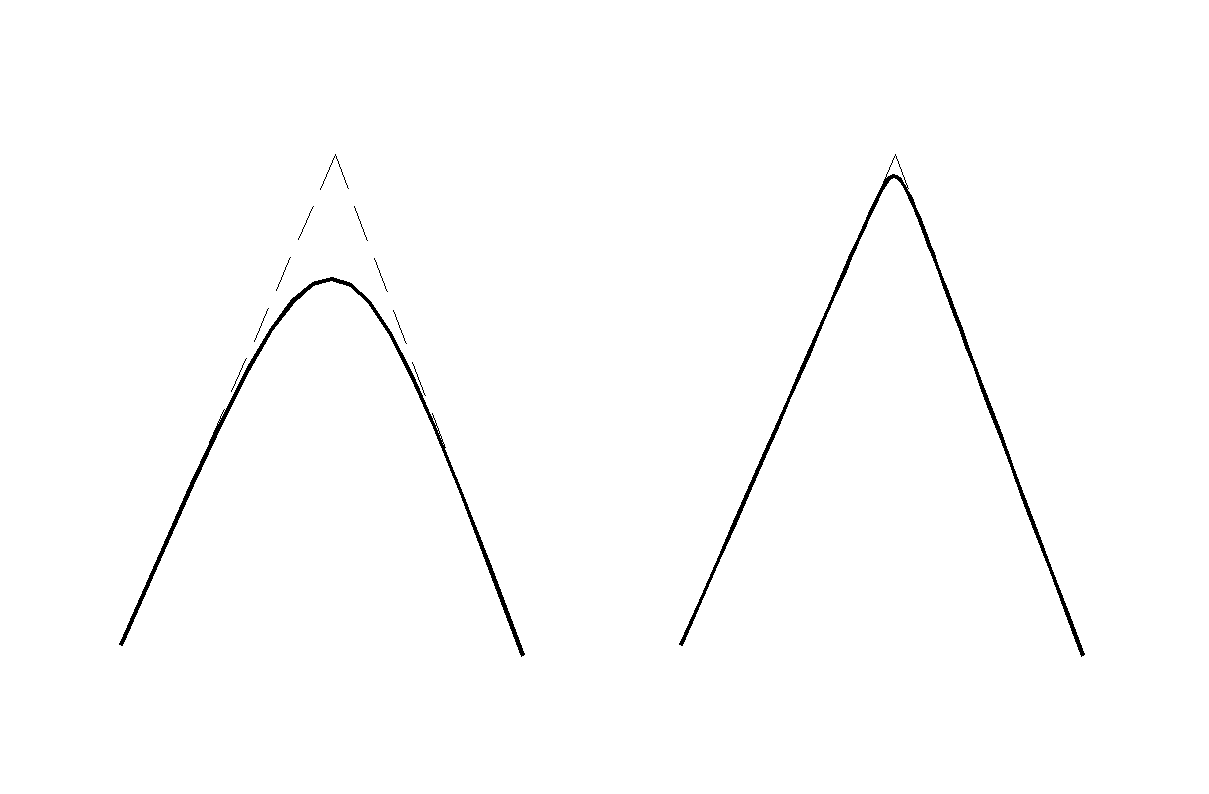
Comportamiento de las B splines con puntos repetidos
Si emplean tres puntos idénticos se obliga a la curva a pasar por ese punto
B spline obligada a pasar por un punto repetido tres veces
La aplicación de las funciones de curvatura para la interpolación y aproximación mediante pequeños segmentos rectos nos permite dibujar curvas que podrían no tener una definición matemática sencilla.
Esta técnica también nos permite emplear los sencillos métodos de transformación e intersección de rectas que veremos más adelante. El mayor inconveniente de este método es el volumen de cálculos necesario para representar incluso una curva sencilla.