DIBUJO ASISTIDO POR ORDENADOR PLANOS Y COORDENADAS

PLANOS Y COORDENADAS

¿Qué es un plano? Las rectas son objetos que tienen una sola dimensión, su longitud. Un plano tiene dos dimensiones, largo y ancho. Podemos conceptualizar un plano como hoja de papel plana, muy delgada que se extiende indefinidamente a lo largo y a lo ancho.

¿Cómo podemos identificar un punto en un plano? Una recta es unidimensional. Sólo es necesario un número para identificar cualquier punto situado sobre ella. Pero la pantalla de una ordenador o una hoja de papel son bidimensionales. Tienen ambos largo y ancho. ¿Cómo podemos entonces identificar un punto en una superficie bidimensional? Una forma de hacerlo es emplear dos rectas diferentes de la superficie que se corten. Por convención estas rectas son perpendiculares, siendo una vertical y otra horizontal. La recta horizontal recibe el nombre de eje x y la recta vertical es el eje y. Como en el caso unidimensional, empleamos estas rectas para medir distancias. El eje x mide la distancia horizontal (a izquierda y derecha) y el eje y mide la distancia vertical (arriba y abajo). El punto donde las dos rectas se cortan es el punto 0 para las dos rectas y se llama origen. Con este esquema podemos identificar cualquier punto situado en una superficie bidimensional empleando dos números. El primer número (denominado coordenada x) mide el alejamiento hacia la derecha del punto desde el origen, sobre el eje x. El segundo número (la coordenada y) mide sobre el eje y el alejamiento en vertical del punto desde el origen. Las coordenadas se escriben como un par ordenado. Por tanto el par (2, 3) especifica un punto que está dos unidades a la derecha y 3 unidades hacia arriba desde el origen. Esta malla rectangular para identificar los puntos recibe el nombre de Sistema Cartesiano de Coordenadas.

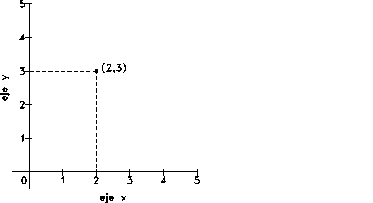
Sistema Cartesiano de Coordenadas

¿Podemos especificar una recta en términos de coordenadas? La respuesta es sí. Consideremos un punto general (x, y) donde x es la coordenada x e y es la coordenada y. Podemos escribir una ecuación en x e y de tal forma que la ecuación sea válida si y sólo si (x,y) es un punto de la recta. Primero, especifiquemos una recta. Recordemos que esto requiere dos puntos diferentes. Sean p₁=(x₁, y₁) y p₂=(x₂, y₂).

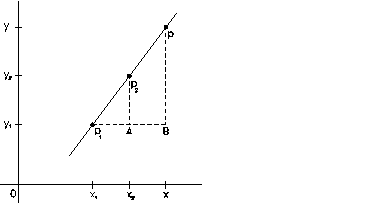
Definición de una recta sobre un plano

Consideremos un tercer punto p=(x,y) que está situado en la recta. Podemos construir dos triángulos que nos ayuden en nuestro estudio. Extendemos una recta horizontal desde p₁. Ya que esta es una recta horizontal, todos los puntos situados en ella tienen la misma coordenada y, que será igual a la del punto p₁, es decir y₁. Si bajamos una recta vertical desde p₂ (todos los puntos de esta recta tienen a x₂ como coordenada x), se cortará con la recta horizontal en el punto A=(x₂, y₁). Una recta vertical trazada desde el punto p corta a la horizontal en el punto B=(x, y₁). Consideremos ahora los dos triángulos, el pequeño p₁p₂A y el grande p₁pB. Estos son dos triángulos semejantes y, por lo tanto, la relación entre los lados semejantes es la misma; es decir, la altura p₂A es a la altura pB como el ancho p₁A es al ancho p₁B. Pero:

Altura p₂A = y₂ - y₁
Altura pB = y - y₁
Ancho p₁A = x₂ - x₁
Ancho p₁B = x - x₁

Entonces, tenemos:

o de otra forma:

y esta es la ecuación de una recta que pasa por los puntos (x₁, y₁) y (x₂, y₂).

Un poco más de álgebra nos permite despejar y para tener:

o

donde

y

La pendiente m es el cambio de altura dividido por la distancia en horizontal entre dos puntos de la recta. La distancia b es la altura a la que la recta corta al eje y. Esto se comprueba fácilmente observando que el punto (0, b) verifica la ecuación de la recta.

¿Podemos determinar el punto de intersección de dos rectas? Si, es bastante fácil determinar donde se cruzan dos rectas. Cuando decimos que dos rectas se cruzan queremos decir que tienen un punto en común. Este punto verifica las ecuaciones de ambas rectas. El problema reside en encontrar ese punto. Supongamos que tenemos las ecuaciones de dos rectas:

recta 1:
recta 2:

Si existe un punto (x_i, y_i) compartido por ambas rectas, entonces las ecuaciones:

serán ciertas. Despejando y_i tenemos:

de donde podemos extraer el valor de x_i:

Llevando este valor a la ecuación de la recta 1 o 2 tenemos:

Por lo tanto, el punto de intersección tendrá por coordenadas:

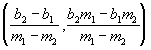
Es importante señalar que dos rectas paralelas tendrán la misma pendiente. Ya que tales rectas no se intersectan, no es extraño comprobar en la expresión anterior que los denominadores se anulan, impidiendo la solución del problema.

Índice