

|
DIBUJO ASISTIDO POR ORDENADOR OCULTAMIENTO DE LÍNEAS Y SUPERFICIES |
OCULTAMIENTO DE LÍNEAS Y SUPERFICIES
Hasta el momento hemos aprendido como construir y proyectar objetos tridimensionales, pero siempre se ven todas las partes del objeto. Esto da a nuestros dibujos una cierta calidad de transparencia. Las figuras que se obtienen de esta forma reciben el nombre de modelos alámbricos ya que sólo presentan los contornos de objetos supuestamente sólidos. Los objetos complejos se pueden convertir rápidamente en un amasijo de segmentos sin sentido. Podría ser difícil identificar que líneas pertenecen a la parte frontal de objeto y cuales están situadas detrás. En este capítulo intentaremos eliminar aquellas líneas que estarían ocultas por alguna de las partes del objeto. Si podemos asignar esta tarea al ordenador, entonces seríamos libres de construir el modelo completo de un objeto (frente, dorso, interior e exterior) y ser capaces todavía de representarlo tal como se vería en la realidad.
Este problema no es tan sencillo como cabría pensar en un principio. De echo, es el más complejo en términos de programación de todos los que veamos en este texto. Lo que naturaleza hace con facilidad (y una gran cantidad de procesamiento paralelo) debemos hacerlo nosotros con un número elevado de cálculos. Existen varias soluciones para el problema de las caras y líneas ocultas. Aquí veremos sólo una de ellas que no es ni la más elegante ni la más eficiente, pero que plantea el problema de una forma directa.
La eliminación de las líneas ocultas de un objeto puede ser un proceso bastante costoso, por lo tanto esto nos obliga a aplicar sencillas comprobaciones para simplificar el problema todo lo que podamos antes de realizar un estudio pormenorizado. Existe una comprobación muy sencilla que eliminará la mayoría de las caras que no se pueden ver. Este test identifica las caras que mirán en la dirección opuesta al observador. Estas son las que constituyen la parte trasera del objeto y no pueden verse porque la masa del objeto se encuentra entre ellas y el observador. Esto, sin embargo, no resuelve la totalidad del problema de la superficies ocultas ya que es posible que la parte delantera del objeto esté oculta por un segundo objeto o por cualquier otra parte del mismo objeto. A pesar de ello, esta comprobación elimina aproximadamente la mitad de las superficies que deben ser verificadas y por tanto simplifica el problema.
Debemos empezar nuestro estudio destacando que sólo las caras poligonales serán motivo de comprobación. Las líneas de por si no pueden ocultar nada, pero aunque podrían estar tapadas, sólo se encuentran como aristas de las caras que definen el objeto. Debido a esto, los polígono son generalmente suficientes para la mayoría de los modelos.
Los polígonos tienen dos caras, la frontal y la dorsal, igual que una hoja de papel. Podemos imaginar nuestros polígono con una cara pintada de color claro y otra pintada de color oscuro. Pero dadas las coordenadas de los vértices de un polígono, ¿cómo podemos saber cuál es cada cara? Fácil, podemos decir que la cara frontal es aquella que se dibuja en sentido horario. Si movemos el punto de vista al lado contrario, de tal forma que la cara oscura sea visible, entonces este mismo polígono parece que se dibuja en sentido antihorario.
Un poco de matemáticas nos permitirá averiguar la dirección hacia la que mira cada una de las caras del objeto (la normal al plano en el que está contenido el polígono). La operación que necesitamos es el producto vectorial. El producto vectorial de dos vectores es otro vector que tiene por módulo el producto de las longitudes de los vectores por el seno del ángulo que forman y, lo más importante para nosotros, una dirección perpendicular al plano que definen estos dos vectores.
![]()
donde
|
|
|
Producto vectorial de dos Vectores
Si tenemos en cuenta, en cualquier pareja de lados de un polígono definen dos vectores en el plano del polígono, entonces el producto vectorial de dos lados del polígono nos da un vector que apunta hacia afuera desde la cara del polígono. ¿Apuntará este vector hacia afuera desde la cara vista o desde la cara oculta del polígono? Eso depende del ángulo que formen los dos lados escogidos, si es cóncavo o convexo.
Supongamos que tenemos dos lados adyacentes que no están sobre la misma línea y que se encuentran en un vértice convexo, es decir, un vértice donde los dos lados se unen formando un ángulo convexo. El producto vectorial nos dará un vector que apunta hacia afuera desde la cara oculta.
Si ahora establecemos la regla de que todos los objetos que construyamos tengan sus caras frontales apuntando hacia el exterior, entonces las caras ocultas estarán en contacto con el material del interior. Esto significa que cuando veamos el objeto desde el exterior, aparecerá dibujado en sentido horario.
Si un polígono es visible, podremos ver su cara frontal y no su cara dorsal, que apuntará en dirección opuesta al observador. Ya que es posible calcular un producto vectorial que nos dice cual es la cara dorsal del polígono, veremos la cara frontal cuando este vector apunte en dirección opuesta al observador. En otro caso, la cara del objeto no es visible y debe ser eliminada.
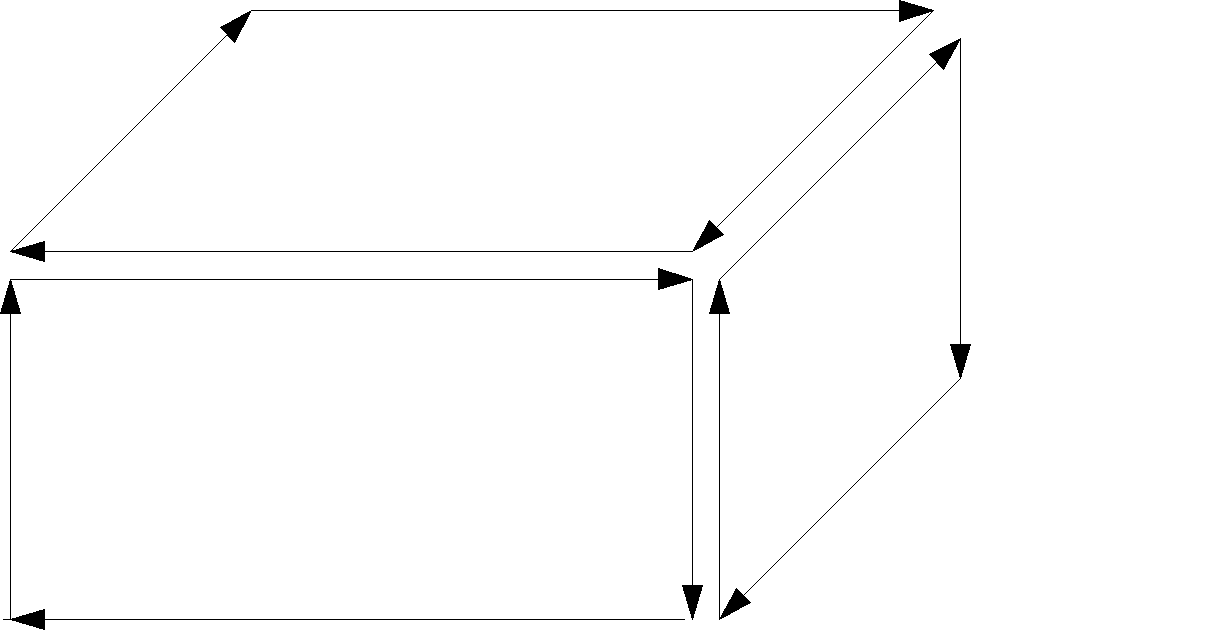
Las caras exteriores de un objeto se dibujan en sentido horario
¿Cómo podemos saber si un vector apunta hacia el observador o no? Este es un problema de comparación de vectores, el vector normal a la superficie y el vector director de la proyección (después de realizar todas las transformaciones del objeto). Para las proyecciones en perspectiva, se puede formar un vector que una el centro de proyección y un punto del polígono. Para una proyección paralela, la dirección de proyección podría servir siempre que apunte desde el objeto hacia el observador. Debemos tener la precaución de indicar de esta forma la dirección cuando empleemos las proyecciones paralelas. Veremos más tarde que la normal al plano de visualización debe apuntar desde el observador hacia el objeto, en dirección contraria a la de proyección.
Tenemos dos vectores (R y S) y queremos comparar sus direcciones. Para hacer esto empleamos su producto escalar
![]()
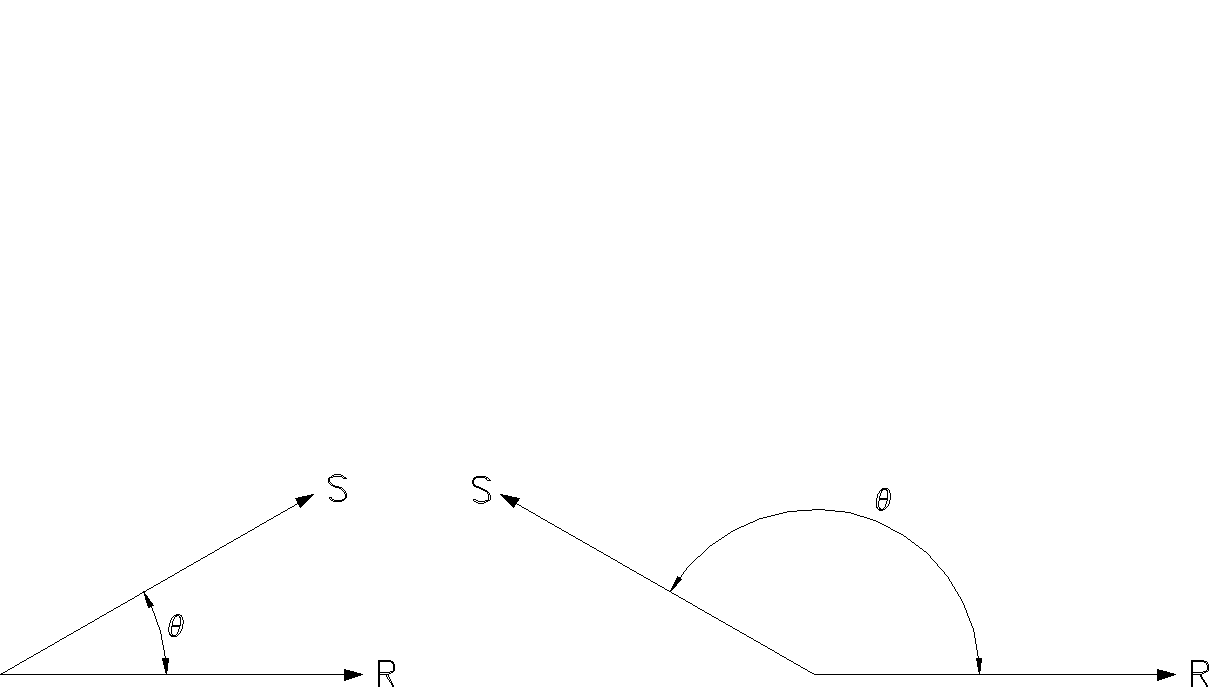
|
cos q > 0 |
cos q < 0 |
El valor del coseno es importante porque si los vectores tienen más o menos la misma dirección (![]() ) entonces es positivo y el producto escalar también lo es; pero si las direcciones son opuestas (
) entonces es positivo y el producto escalar también lo es; pero si las direcciones son opuestas (![]() ), el coseno es negativo y también el producto escalar.
), el coseno es negativo y también el producto escalar.
Para determinar si un polígono es una cara frontal o dorsal del objeto, utilizamos el producto vectorial para determinar su normal y luego calculamos el producto escalar con el vector de proyección. Un valor negativo significa que la cara dorsal mira en dirección opuesta a la del observador y, por tanto, la cara frontal puede ser observada. La expresión para determinar el valor del producto escalar es
![]()
Por lo tanto, la comprobación de ocultamiento de la cara se reduce a la determinación del signo de a.
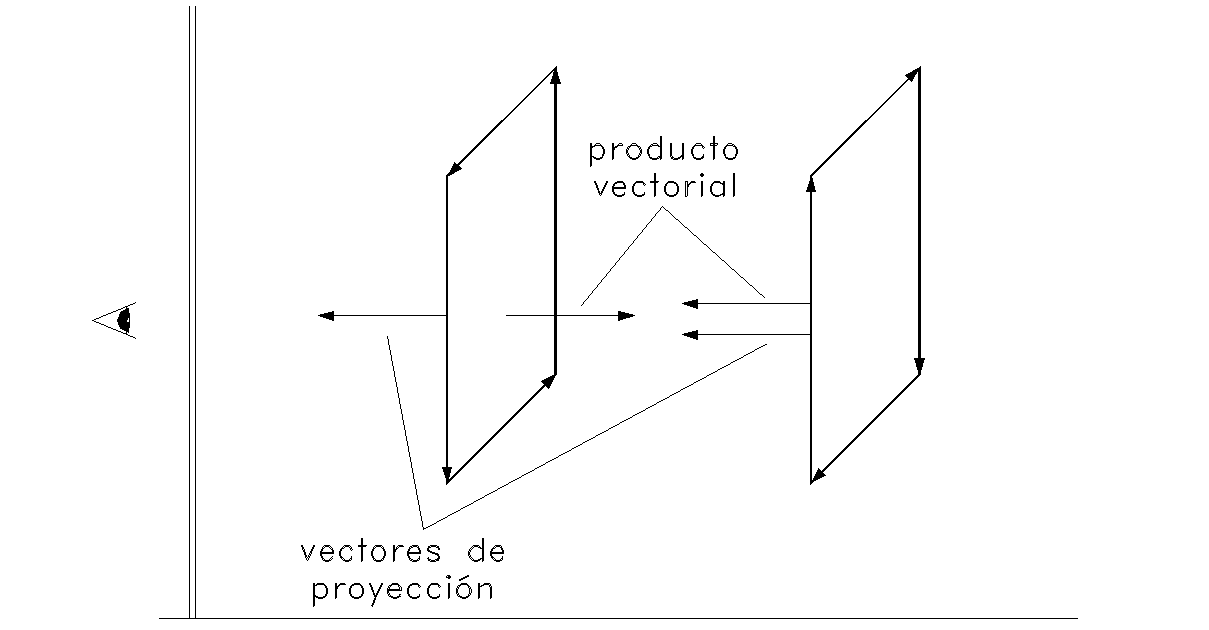
El plano de la izquierda será visible (a
<0) mientras que el derecho está oculto (a>0)Debemos tener cuidado a la hora de elegir los lados del polígono P y Q. Estos vectores deben formar un ángulo convexo. ¿Cómo encontramos este ángulo convexo? Fácil, seleccionamos un extremo del polígono como el punto que está más a la derecha o más a la izquierda o más arriba. Con los dos puntos anterior y posterior al escogido definimos los dos vectores que necesitamos, comprobando que los tres puntos no están alineados. Si ocurre que el tercer punto está alineado con los dos primeros, se escoge el siguiente vértice del polígono y se intenta de nuevo. Se usamos todos los vértices del polígono sin éxito, entonces se trata de una línea simplemente y puede ser descartado sin más.
Todas estas transformaciones deben realizarse justo antes de proyectar el objeto sobre el plano de visualización.
Aunque el algoritmo que hemos visto en el apartado anterior puede eliminar muchas de las caras y líneas ocultas, no resuelve completamente el problema. Si tenemos dos objetos separados, entonces alguna de la caras vistas de uno de ellos podría ocultar parcialmente alguna de las caras vistas del otro.
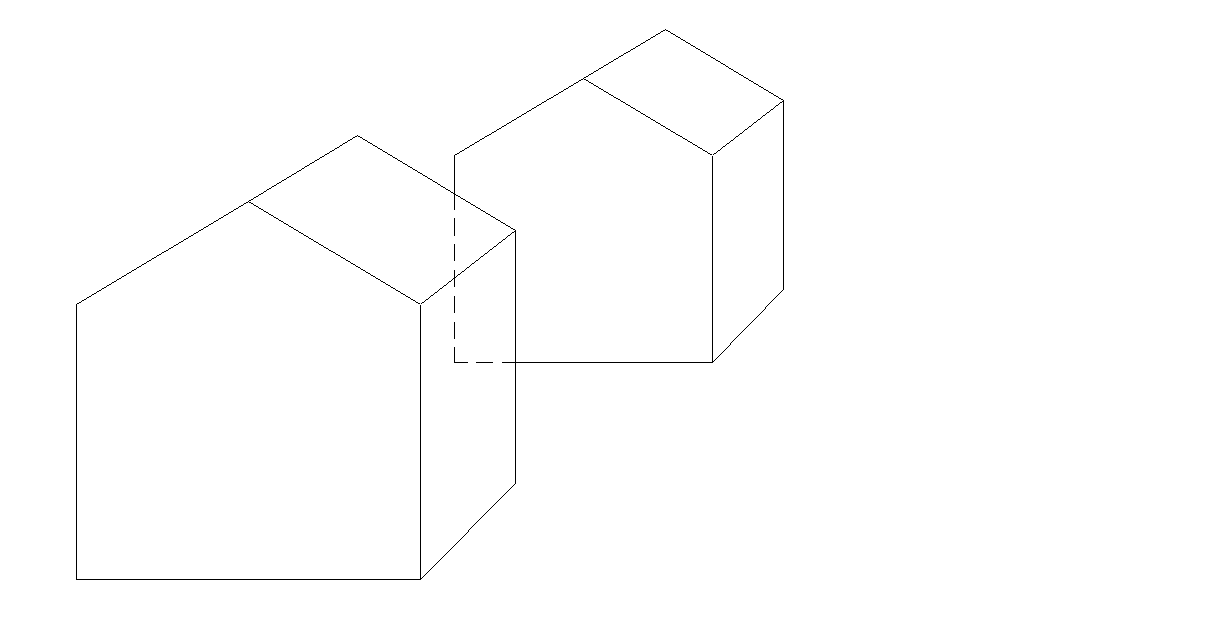
Líneas ocultas por caras vistas
El algoritmo que veremos a continuación resuelve este problema para superficies convexas en dispositivos raster. Para ello se hace uso de algunas propiedades de este tipo de dispositivos. Sólo tendremos en cuenta polígonos con su interior relleno.
El algoritmo recibe su nombre por la forma en que un pintor crea un óleo. El artista empieza pintando el fondo para luego dibujar los objetos del frente. No es necesario borrar determinadas partes del fondo, el artista simplemente pinta encima de ellas. La nueva pintura cubre a la vieja de tal forma que sólo es visible la última capa de pintura.
Los dispositivos raster tienen esta misma propiedad. Un polígono relleno se representa cambiando el color de los pixel correspondientes a su interior. Si dibujamos un segundo polígono encima del primero, algunos de estos mismos puntos cambiarán para reflejar el interior del segundo polígono. Esto implica que primero debemos dibujar los polígonos que están más lejos del observador, dejando para el final los que están más cerca del observador. De esta forma, las superficies se cubren si ordenamos correctamente los polígonos antes de dibujarlos.
En el apartado anterior trabajamos con polígonos rellenos para eliminar las caras ocultas. Veremos ahora como podemos eliminar los lados ocultos de los polígonos cuando no podemos recurrir al algoritmo del pintor.
Así, examinaremos todos y cada uno de los lados de los polígonos que constituyen el objeto antes de dibujarlos en pantalla. Compararemos cada lado con todos los triángulos (previamente se habrán descompuesto los polígonos en triángulos para facilitar los cálculos) que están situados enfrente de él para comprobar si está parcial o totalmente oculto.
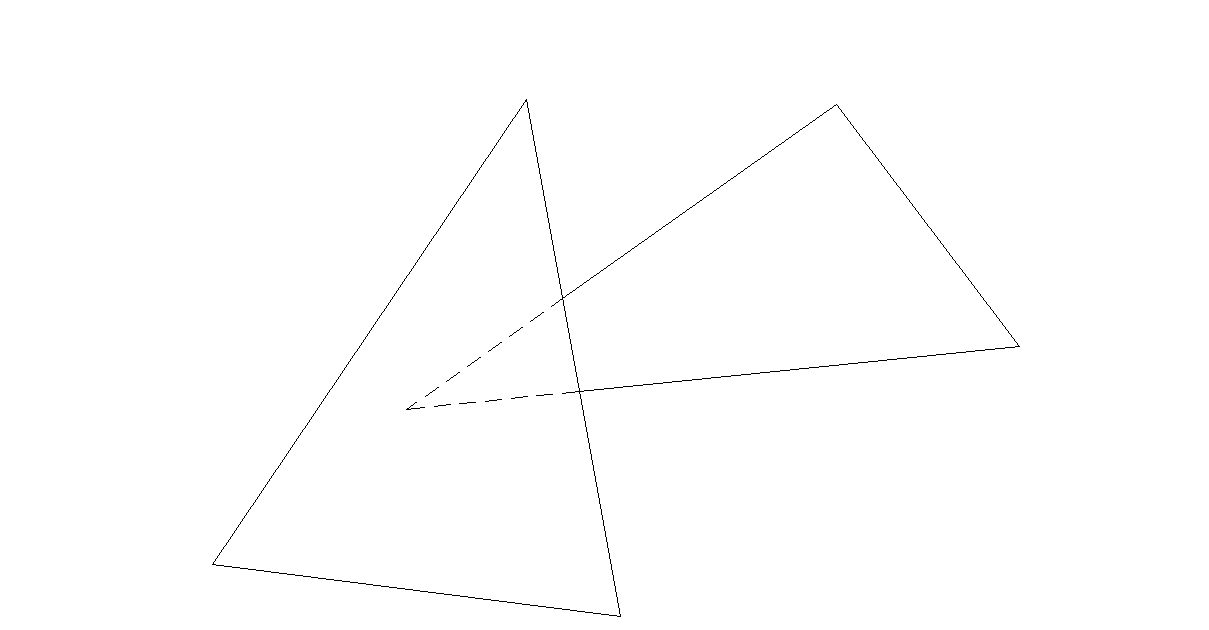
Segmentos eliminados por ocultamiento
Un triángulo puede ocultar a un segmento de varias formas diferentes. Si los dos extremos del segmento están dentro del triángulo, entonces todo el segmento es invisible.
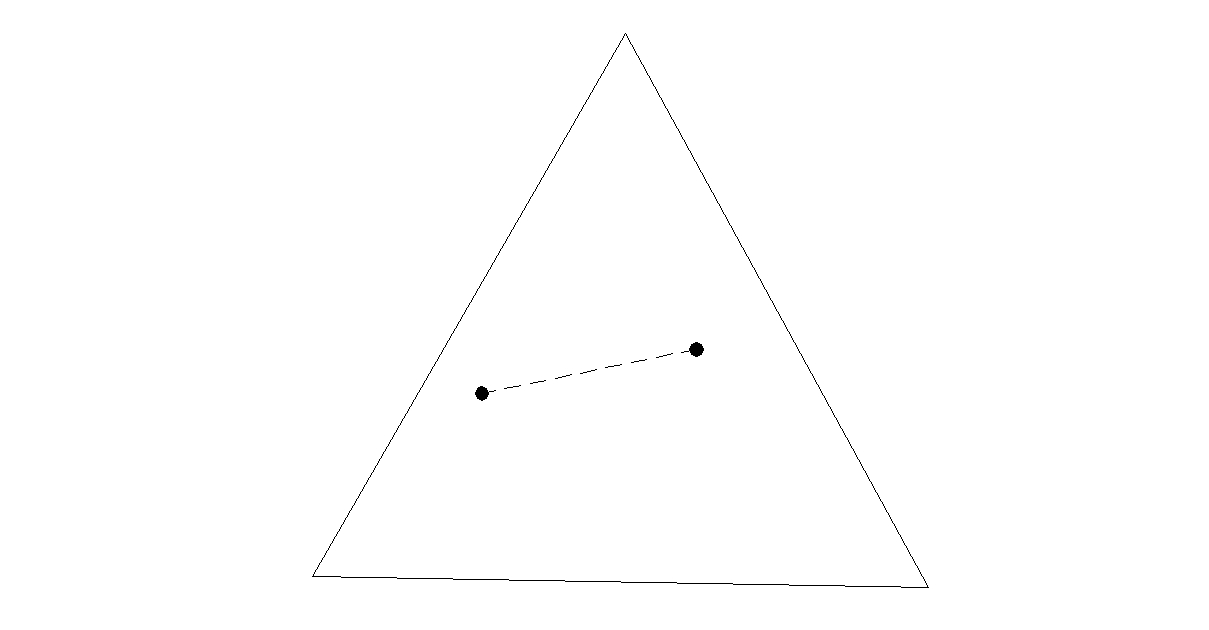
Si los dos extremos están en el interior del triángulo el segmento es invisible
Si un extremo está dentro del triángulo y otro en el exterior sólo una parte del segmento será invisible. En este caso debemos comprobar los tres lados del triángulo para determinar la intersección del segmento con alguno de ellos. El punto de intersección divide el segmento en dos partes. La parte que queda dentro del triángulo será invisible, mientras que la otra porción es todavía visible y debe comprobarse si la oculta algún otro triángulo.
Si un extremo está dentro y otro fuera del triángulo, sólo una porción es invisible
Si los dos puntos están fuera del triángulo, existen dos posibilidades. En un caso, el segmento está totalmente fuera del triángulo. En este caso, el segmento es visible en su totalidad (a no ser que lo oculte otro triángulo). En el segundo caso, el segmento entra y sale del triángulo, es decir, corta a dos de los lados del triángulo, quedando dividido en tres partes. La porción central estará oculta, mientras que las otras dos deben ser comprobadas con el resto de triángulos.
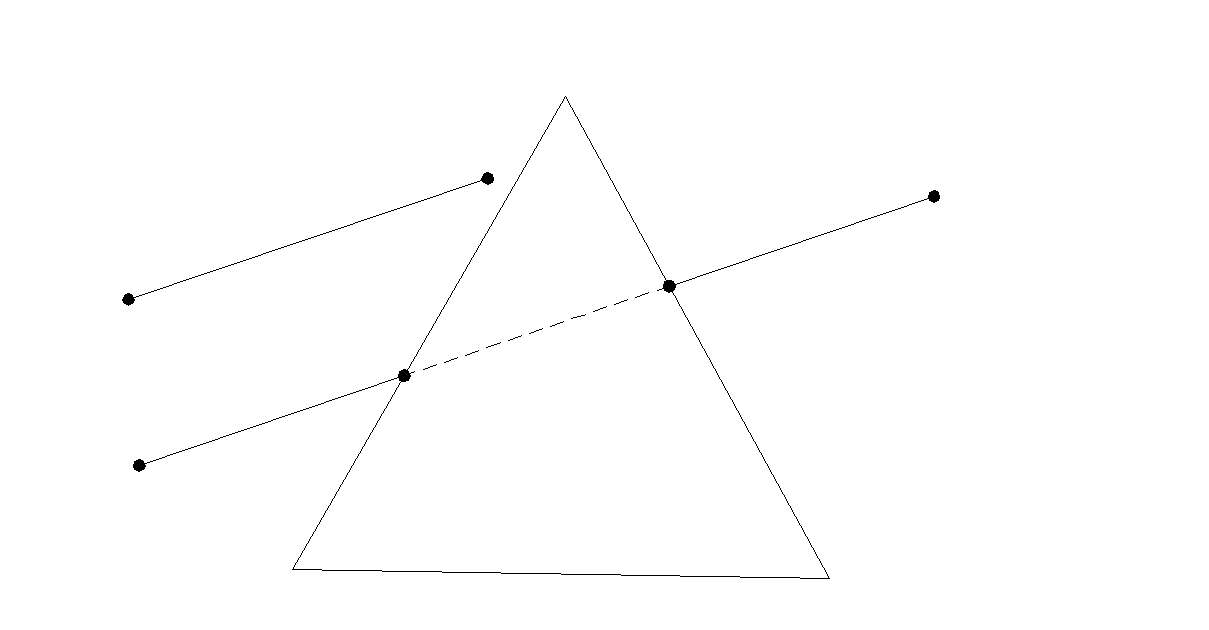
Los dos extremos están fuera del triángulo, puede haber o no intersección
A pesar de todas las comprobaciones realizadas existen caso todavía que no pueden ser tratados con estos algoritmos.
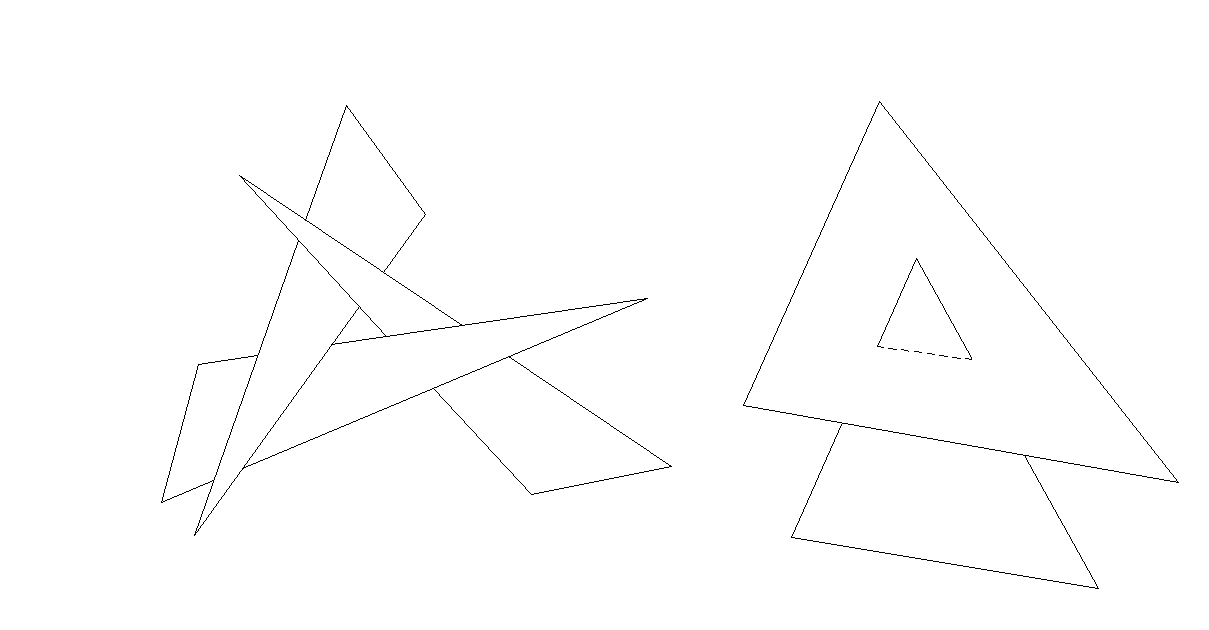
Casos que no pueden ser manejados con las técnicas presentadas
GNUPLOT: UN PROGRAMA PARA REPRESENTACIÓN DE FUNCIONES
GNUPLOT es un programa interactivo de representación de funciones. Puede ser ejecutado en diferentes plataformas (UNIX, Windows, MSDOS, VMS, etc.) y es gratis, a pesar de estar sometido a las leyes de propiedad intelectual. Soporta, además, muchos tipos diferentes de terminales, trazadores e impresoras (incluyendo muchos dispositivos en color). Maneja tanto curvas (2 dimensiones) como superficies (3 dimensiones).
Las superficies pueden ser presentadas mediante una malla cuadrada que se ajusta a la función especificada en el espacio tridimensional de coordenadas, o como un mapa de isolíneas situado en el plano xy. Para los dibujos 2D existen múltiples tipos de diseños incluyendo líneas, puntos, líneas con puntos, barras de error e impulsos (puros gráficos de barras). Los gráficos pueden ser etiquetados por el usuario. El programa incluye en la mayoría de las plataformas la capacidad de editar las líneas de comandos.
Este programa distingue entre mayúsculas y minúsculas (los comandos y nombre de funciones escritos en minúsculas no son los mismos que los escritos con mayúsculas). Todos los comandos pueden ser abreviados, mientras que la abreviación no sea ambigua. En una misma línea de comando pueden aparecer varios comandos, siempre que este separados por punto y coma (;). Las cadenas se presentan entre comillas, que pueden ser dobles (") o sencillas (‘). Por ejemplo
Los argumentos que se pasan en la línea de comandos se supone que son nombres de ficheros que contienen comandos de GNUPLOT, con la excepción de los argumentos estándar X11, que se procesan en primer lugar. Cada fichero se carga con el comando load, según el orden establecido. GNUPLOT termina después de que el último fichero ha sido procesado. Cuando no se indica ningún fichero para ser cargado, entonces GNUPLOT arranca en el modo interactivo.
Los comandos se pueden extender a lo largo de varias líneas, siempre que cada una de las líneas termina con una barra invertida (\). La barra invertida debe ser el último de los caracteres de cada línea. El efecto es el mismo que si no estuviesen allí la barra invertida y el salto de línea. Es decir, no se incluye ningún espacio en blanco, ni se terminan los comentarios. Por lo tanto, comentar una línea que continua en la siguiente supone eliminar todo el comando (ver comment)
En este capítulo, las llaves ({}) indican argumentos opcionales en muchos de los comandos, y una barra vertical (|) separa opciones mutuamente excluyentes. Las palabras claves de GNUPLOT se indican en negrita. Los símbolos (<>) se utilizan para indicar elementos reemplazables.
En la versión Windows, como se aprecia en la siguiente figura, los diferentes comandos y opciones se han implementado mediante menús desplegables. A medida que se van escogiendo las opciones desde el menú correspondiente, estas aparecen en la línea de comandos. Es posible, también, teclear directamente el comando deseado, tal como se haría en el resto de plataformas.
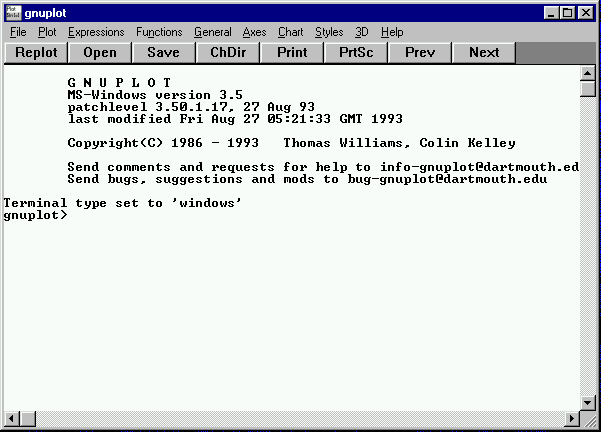
Pantalla principal de la versión para Windows de GNUPlot
Algunos comandos, de uso más frecuente, se presentan en una botonera especial que facilita el acceso a ellos.
![]()
Botonera de acceso rápido a los comandos más frecuentes
replot
: redibuja el último gráfico creado con plot o splotopen
: despliega el diálogo de lectura de ficheros de comandossave
: despliega el diálogo de escritura de ficheros de comandoschdir
: cambia el directorio de trabajoprtsc
: copia la ventana gráfica en el dispositivo seleccionadoprev
: muestra el anterior comando de la listanext
: muestra el siguiente comando de la listaAsí, las opciones de leer y grabar ficheros hacen uso de las ventanas de diálogo tan frecuentes en Windows y que son comunes a todas las aplicaciones que se ejecutan en este entorno.
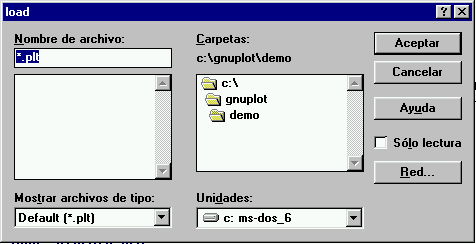
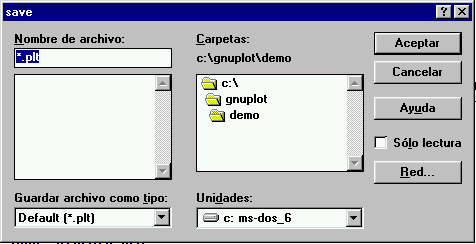
Diálogo para la lectura y escritura de ficheros de comandos
También, las posibilidades de imprimir los gráficos generados con GNUPLOT mejoran sensiblemente gracias a la utilización de los dispositivos de impresión instalados en Windows. De este modo, la ventana donde se presentan los gráficos dispone de un menú de opciones que permite al usuario modificar de forma interactiva distintas opciones (tipo de letra, tipos de líneas, etc), así como crear una copia en papel del gráfico creado. No debemos olvidar tampoco las posibilidades que ofrece Windows para incluir los gráficos generados por GNUPLOT en otras aplicaciones (procesadores de texto, hojas de cálculo, etc.) que se ejecutan en este sistema operativo.

Menú de opciones de la venta gráfica de GNUPLOT
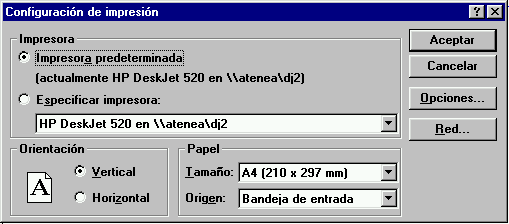
Menú de configuración de la impresora
Para empezar veremos los comandos plot y splot, que son el núcleo del programa. Son los encargados de representar las funciones en un montón de formas diferentes. plot se emplea para representar funciones y datos 2D, mientras que splot se utiliza para funciones y datos 3D.
Sintáxis:
donde se indica una <función> o el nombre de un fichero de datos entre comillas. Una función es una expresión matemática, o un par (plot) o una tripleta (splot) de expresiones matemáticas en el caso de funciones paramétricas. Por supuesto, también es posible definir nuevas funciones (de 1 a 5 variables) o constantes en cualquier momento. La sintaxis para la definición de funciones es:
donde <expresión> está definida en función de las variables <var1>, <var2> hasta <var5>. La sintaxis para definición de constantes es
Ejemplos de funciones definidas por el usuario:
w = 2
q = floor(tan(pi/2 - 0.1))
f(x) = sin(w*x)
sinc(x) = sin(pi*x)/(pi*x)
delta(t) = (t == 0)
ramp(t) = (t > 0) ? t : 0
min(a,b) = (a < b) ? a : b
comb(n,k) = n!/(k!*(n-k)!)
len3d(x,y,z) = sqrt(x*x+y*y+z*z)
Los comandos plot y splot pueden ser tan sencillos como
plot sin(x)
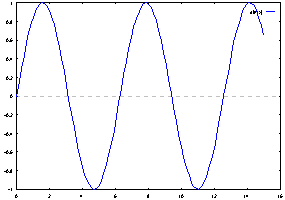
y
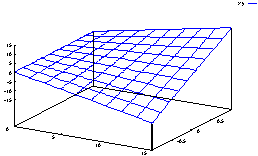
o tan complejo como
aquí la expresión [t=1:10] le dice a GNUPLOT que el parámetro t varía entre 1 y 10, mientras que [-pi:pi*2] indica que sólo se van a presentar los valores de la función comprendidos en este rango. Separadas por comas, en este comando aparecen tres funciones; el segundo de los gráficos se obtiene al representar como x los valores contenidos en la segunda columna del fichero data.1 y como variable dependiente los contenidos en la tercera columna. En cada caso la opción with indica el tipo de representación escogida para cada función. Tanto la constante pi como la función tan() están definidas dentro del programa.
En la siguiente tabla se recogen todas las funciones definidas dentro de GNUPLOT.
|
abs |
acos |
arg |
asin |
atan |
besj0 |
besj1 |
|
besy0 |
besy1 |
ceil |
cos |
cosh |
erf |
erfc |
|
exp |
floor |
gamma |
ibeta |
inverf |
igamma |
imag |
|
invnorm |
int |
lgamma |
log |
log10 |
norm |
rand |
|
real |
sgn |
sin |
sinh |
sqrt |
tan |
tanh |
Por otro lado, GNUPLOT facilita al usuario toda la ayuda necesaria para el correcto funcionamiento del programa. Para ello sólo es necesario teclear ? o help en la línea de comandos.
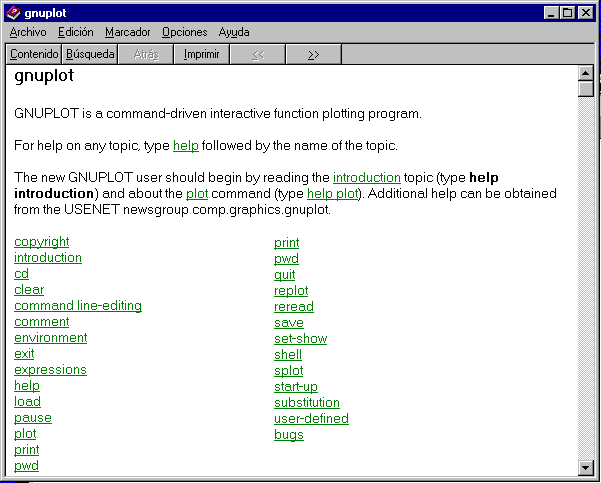
Ventana de ayuda de GNUPLOT bajo Windows
También es posible evaluar expresiones sin necesidad de crear ningún gráfico, esto convierte a GNUPLOT en una potente calculadora. Para ello solo es necesario utilizar el comando print.
gnuplot> print cos(pi/4)
0.707107
gnuplot> print exp(-0.5*(1.96)**2)/sqrt(2*pi)
0.0584409
Para completar esta capacidad, debemos tener en cuenta también que uno de los múltiples tipos de terminales de los que dispone el programa, en vez de representar gráficamente el resultado de un comando plot/splot, crea un tabla con los valores de x, f(x) para plot y x, y, f(x,y) para splot.
gnuplot> set samples 10
gnuplot> set term table
Terminal type set to 'table'
gnuplot> plot [0:pi] sin(x)
Curve 0, 10 points
i x=0 y=0
i x=0.349066 y=0.34202
i x=0.698132 y=0.642788
i x=1.0472 y=0.866025
i x=1.39626 y=0.984808
i x=1.74533 y=0.984808
i x=2.0944 y=0.866025
i x=2.44346 y=0.642788
i x=2.79253 y=0.34202
i x=3.14159 y=0
Otras posibilidades interesantes de GNUPLOT son la creación de isolíneas y la eliminación de líneas ocultas. En el primer caso se debe activar esta opción haciendo uso del comando:
set contour { base | surface | both }
set nocontour
Si no se especifica ninguna opción, por defecto se toma base. Estas tres opciones indican la posición que van a ocupar las isolíneas en el dibujo:
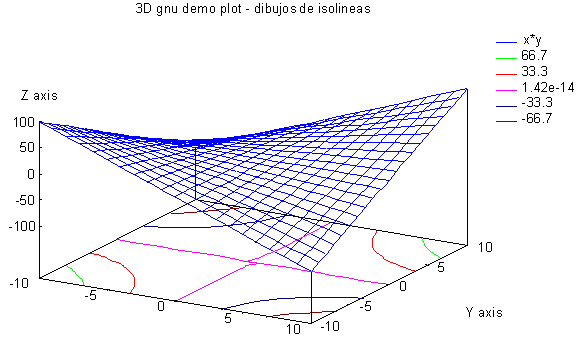
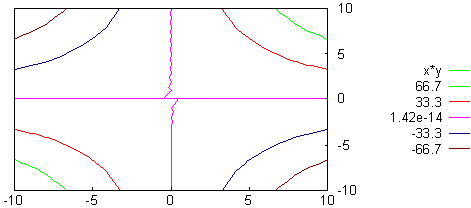
Por lo que se refiere a la eliminación de líneas ocultas esta opción se activa mediante el comando:
set hidden3d
set nohidden3d
show hidden3d
Todas las superficies dibujadas se ven afectadas por este comando, eliminándose las partes ocultas incluso por otras superficies. Esta opción sólo tiene sentido cuando las superficies se representan mediante retículas.
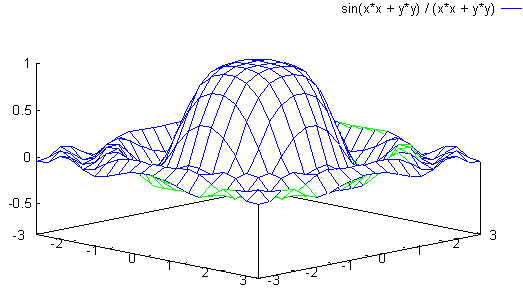
Ejemplo de eliminación de líneas ocultas
LISTADO 7 - OCULTACIÓN DE CARAS EN OBJETOS TRIDIMENSIONALES
En el siguiente listado se presenta un programa que lee desde un fichero, suministrado por el usuario, la definición de un objeto. En la primera línea de este fichero se indican el número de puntos, elementos y vértices que componen el objeto. En las siguientes líneas se indican las coordenadas de los puntos y los índices de los vértices que constituyen cada una de las caras poligonales del objeto. Por último, se ordenan las caras del objeto de tal forma que se dibujan primero las más alejadas del observador.
Debido al número de cálculos necesarios se ha escogido para la realización de este programa el lenguaje C.
Resultado de la ejecución:

