

|
DIBUJO ASISTIDO POR ORDENADOR INTERPOLACIÓN |
¿Cómo podemos expresar una curva que no tiene una definición matemática sencilla? Podemos dibujar una aproximación de dicha curva si tenemos un conjunto de puntos representativos. Podemos luego adivinar el comportamiento que debería tener la curva entre los puntos anteriores. Si la curva es suave y los puntos representativos están los suficientemente juntos, podemos hacer una buena aproximación de las partes que faltan de la curva. Nuestra predicción no será exacta, pero bastará para guardar las apariencias. Llenaremos las partes desconocidas de la curva con porciones de curvas conocidas que pasan por los puntos que la definen. Ya que la curva desconocida y la conocida comparten los mismo puntos localmente, suponemos que en esas zonas las dos son bastante parecidas. Ajustamos una porción de la curva que no conocemos con una curva que conocemos. Así podemos rellenar los huecos existentes entre los puntos de partida determinado las coordenadas de los puntos que pertenecen a la curva conocida o aproximante y uniendo estos puntos con segmentos de recta.
La siguiente pregunta que nos hacemos es ¿qué curva empleamos como aproximación? ¿cuál es la expresión matemática de la curva que pasa por varios puntos en una determinada región? Existen muchas funciones que se pueden hacer pasar por un determinado número de puntos mediante el ajuste de los parámetros que las caracterizan. Se han empleado las funciones trigonométricas, polinómicas, exponenciales y otros tipos. Es más, dentro de cada clase existen múltiples opciones. Nosotros utilizaremos las funciones polinómicas para realizar la aproximación de la curva.
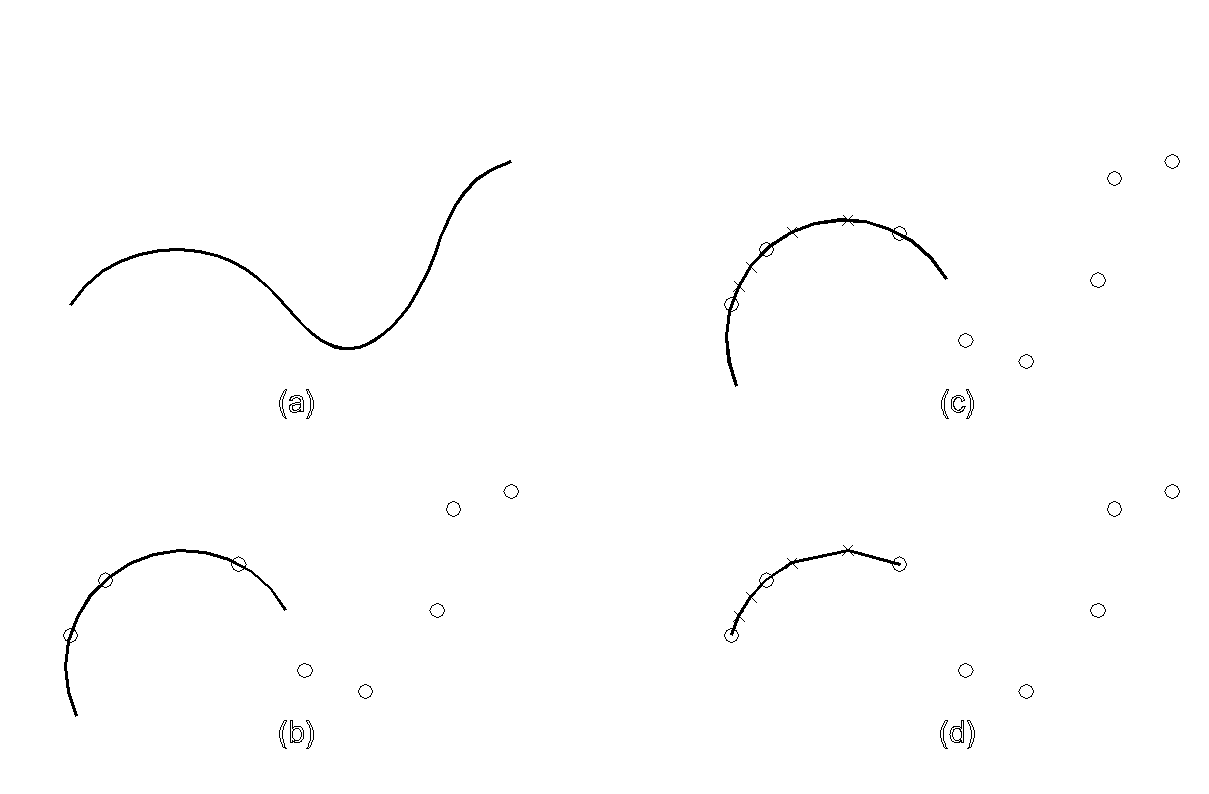
Figura 1.- Proceso de Interpolación
curva desconocida a aproximar
ajustamos una región con una curva conocida
calculamos más puntos a partir de la curva conocida
dibujamos los segmentos de recta que conecta todos los puntos
Las funciones se suelen expresar frecuentemente de la forma ![]() , pero nosotros preferimos la forma paramétrica:
, pero nosotros preferimos la forma paramétrica:
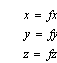
Existen un par de razones por las que la forma paramétrica es preferible. Por un lado, la diferencia entre dos y tres dimensiones sólo supone añadir una tercera ecuación para z. Trata las tres direcciones de forma similar y permite valores múltiples (varios valores de y para un mismo valor de x) de tal forma que las curvas pueden volver sobre si mismas o incluso cortarse.
Inventemos ahora una función que pueda ser empleada en la interpolación. Habrá un montón de cosas mal en este primer intento, pero a pesar de ello nos servirá para comprender mejor este planteamiento.
Supongamos que necesitamos una curva polinómica que para por un determinado número n de puntos
![]()
Construiremos la función de acuerdo a los siguientes sumatorios, un término por cada uno de los puntos de referencia.
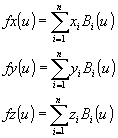
Las funciones
![]() reciben el nombre de
funciones de curvatura. Para cada valor del parámetro
u indican cuanto afecta el punto
i a la posición de la curva. Podemos imaginar que cada punto intenta atraer la curva hacia si mismo. La función
reciben el nombre de
funciones de curvatura. Para cada valor del parámetro
u indican cuanto afecta el punto
i a la posición de la curva. Podemos imaginar que cada punto intenta atraer la curva hacia si mismo. La función
![]() nos dice como es de fuerte esta atracción. Si para algún valor de u
,
nos dice como es de fuerte esta atracción. Si para algún valor de u
, ![]() y para
cada
y para
cada ![]() ,
,
![]() , entonces el punto
i tiene el control completo sobre la curva. La curva pasará por el punto i. Si, para un valor diferente del parámetro, otro punto tiene el control de la curva,
también pasará la curva por él. Lo que necesitamos
entonces son funciones de curvatura que para diferentes valores de
u den sucesivamente el control de la curva a cada uno de los puntos de referencia o puntos de control.
, entonces el punto
i tiene el control completo sobre la curva. La curva pasará por el punto i. Si, para un valor diferente del parámetro, otro punto tiene el control de la curva,
también pasará la curva por él. Lo que necesitamos
entonces son funciones de curvatura que para diferentes valores de
u den sucesivamente el control de la curva a cada uno de los puntos de referencia o puntos de control.
Los valores particulares del parámetro u para los que la curva pasa por los puntos de control no
tienen demasiada importancia, siempre que los puntos de referencia tomen el control de la curva en el orden correcto. Debemos crear funciones de curvatura para las que el primer punto de referencia
![]() tiene el control total cuando
tiene el control total cuando ![]() , el segundo cuando
, el segundo cuando
![]() , el tercero cuando
, el tercero cuando
![]() y así sucesivamente.
La razón para esta elección de los valores de u es hacer más fácil la implementación del
programa. Para esto necesitamos que
y así sucesivamente.
La razón para esta elección de los valores de u es hacer más fácil la implementación del
programa. Para esto necesitamos que
![]() valga 1 cuando
valga 1 cuando
![]() , y 0 para
, y 0 para
![]() . Una expresión que es nula en los puntos correctos es:
. Una expresión que es nula en los puntos correctos es:
![]()
Para ![]() esta expresión vale
esta expresión vale
![]()
por tanto, si dividimos por esta constante tenemos un valor unitario para ![]() , que es precisamente el comportamiento que buscamos
, que es precisamente el comportamiento que buscamos
![]()
La función de curvatura i-ésima se puede construir de la misma forma para que tome el valor 1 en ![]() y sea nula para el resto de los enteros.
y sea nula para el resto de los enteros.
![]()
Consideremos el caso donde existen cuatro puntos de control. Serán necesarias por tanto cuatro funciones de curvatura. La expresión anterior nos da las siguientes funciones:
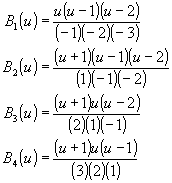
Utilizando estas funciones y los cuatro puntos de control se puede construir una curva que pase por los cuatro.
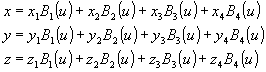
Ahora se espera que esta curva se acerque bastante a la curva real en la región correspondiente a estos cuatro puntos, particularmente en el medio, entre el segundo y el tercero. Esta es la zona de la curva que se obtiene para valores de u comprendidos entre 0 y 1. Podemos encontrar los puntos de curva aproximada dando valores a u dentro de ese rango. Los resultados de estos cálculos nos permiten obtener las coordenadas de los segmentos que luego podrán ser dibujados como representación de dicha curva aproximada. Por ejemplo, supongamos que deseamos aproximar la curva entre el segundo y el tercer punto de referencia mediante tres segmentos rectos. Tenemos como puntos válidos los obtenidos para ![]() y
y ![]() . Si utilizamos nuestras ecuaciones para calcular los puntos en
. Si utilizamos nuestras ecuaciones para calcular los puntos en ![]() y
y ![]() , tendremos cuatro puntos que nos sirven como extremos de los tres segmentos aproximados. Siguiendo este mismo proceso podemos aproximar toda la curva. Tomamos cuatro puntos de control consecutivos (1, 2, 3, 4) y aproximamos el tramo comprendido entre los dos del medio (2, 3). Damos ahora un paso más, y nos desplazamos al siguiente punto de control en un extremo y descartamos el último por el otro lado (2, 3, 4, 5). Podemos aproximar entonces la siguiente porción de la curva (3, 4). De esta forma nos movemos por todos los puntos de control hasta dibujar la curva completa. Las regiones inicial y final de la curva requieren un tratamiento especial. Para los primeros cuatro puntos (1, 2, 3, 4) necesitaremos dibujar la región comprendida entre los puntos 1 y 2 dando valores a u entre -1 y 0. De igual forma, la función de curvatura para la última etapa del proceso debe ser evaluada para valores de u entre - y 2. No existe nada particularmente difícil en estos casos especiales, sólo debemos tenerlos en cuenta.
, tendremos cuatro puntos que nos sirven como extremos de los tres segmentos aproximados. Siguiendo este mismo proceso podemos aproximar toda la curva. Tomamos cuatro puntos de control consecutivos (1, 2, 3, 4) y aproximamos el tramo comprendido entre los dos del medio (2, 3). Damos ahora un paso más, y nos desplazamos al siguiente punto de control en un extremo y descartamos el último por el otro lado (2, 3, 4, 5). Podemos aproximar entonces la siguiente porción de la curva (3, 4). De esta forma nos movemos por todos los puntos de control hasta dibujar la curva completa. Las regiones inicial y final de la curva requieren un tratamiento especial. Para los primeros cuatro puntos (1, 2, 3, 4) necesitaremos dibujar la región comprendida entre los puntos 1 y 2 dando valores a u entre -1 y 0. De igual forma, la función de curvatura para la última etapa del proceso debe ser evaluada para valores de u entre - y 2. No existe nada particularmente difícil en estos casos especiales, sólo debemos tenerlos en cuenta.