

|
DIBUJO ASISTIDO POR ORDENADOR FOTOREALISMO |
FOTOREALISMO
INTRODUCCIÓN
En el capítulo anterior hemos visto como construir objetos utilizando caras poligonales. Somos capaces ahora de proyectar y representar imágenes en perspectiva de objetos para obtener una idea de profundidad. Hemos visto también como eliminar las líneas y las superficies ocultas de los objetos para dar a las imágenes un aspecto más realista. Los polígonos que constituyen los objetos pueden ser sombreados. Generalmente, será posible dibujar polígonos con diferentes tramas de relleno, consiguiendo de esta forma reflejar los diferentes tonos de color que tienen las superficies del objeto.
Consideremos primero una fuente de luz indirecta. Supondremos que nuestro objeto está iluminado por una luz que no proviene de una fuente en particular de luz si no que ilumina al objeto desde todas las direcciones. Esta recibe el nombre de luz de fondo, luz que es reflejada por las paredes, suelo y techo. Suponemos que esta luz es uniforme, que tiene la misma intensidad en todos los puntos. No habrá puntos brillantes ni una dirección predominante. De esta forma cualquier superficie del objeto recibe la misma intensidad de luz difusa sea cual sea su orientación espacial.
De toda la luz que incide sobre el objeto, una porción es absorbida por su superficie mientras que el resto es reflejado o reemitido. La proporción de luz reflejada respecto al total recibe el nombre de coeficiente de reflexión o reflectividad. Una superficie blanca refleja casi la totalidad de la luz que incide sobre ella, es decir, su coeficiente de reflexión es próximo a 1. Una superficie negra, por el contrario, absorbe la mayor parte de la luz que llega a ella, es decir, su reflectividad es casi nula. Una superficie color gris tendrá un coeficiente de reflexión intermedio. La mayor parte de los objetos reflejan unos colores mejor que otros. Por ejemplo, si un objeto tiene una elevada reflectividad para el color rojo y valores pequeños para el resto de colores, entonces dicho objeto se verá de color rojo. Si empleamos un monitor en color que da a cada punto de la pantalla diferentes intensidades de verde, rojo y azul, deberemos especificar tres valores de reflectividad con el fin de conocer las características de color y sombra del objeto. Pero para que las cosas no sean demasiado complicadas sólo tendremos en cuenta los monitores con tonos de gris. Así un único coeficiente de reflexión (R) nos indicará el tono de gris del objeto que vamos a representar.
Hemos supuesto que la cantidad de luz que incide sobre el objeto no cambia con la posición de este porque la luz proviene uniformemente de todas las direcciones, pero ¿varía la cantidad de luz reflejada hacia nuestros ojos con las diferentes orientaciones? La respuesta es que el objeto se verá igual de brillante independientemente de su posición. Este resultado se produce por la cancelación de dos efectos. El primer efecto es que se emite más luz en la dirección perpendicular a la superficie que en la dirección paralela a ella. La relación exacta entre las dos direcciones recibe el nombre de Ley de Lambert, y establece que la reflexión de la luz por una superficie perfectamente difusora varía con el coseno del ángulo que forman la normal a la superficie y la dirección del rayo reflejado.
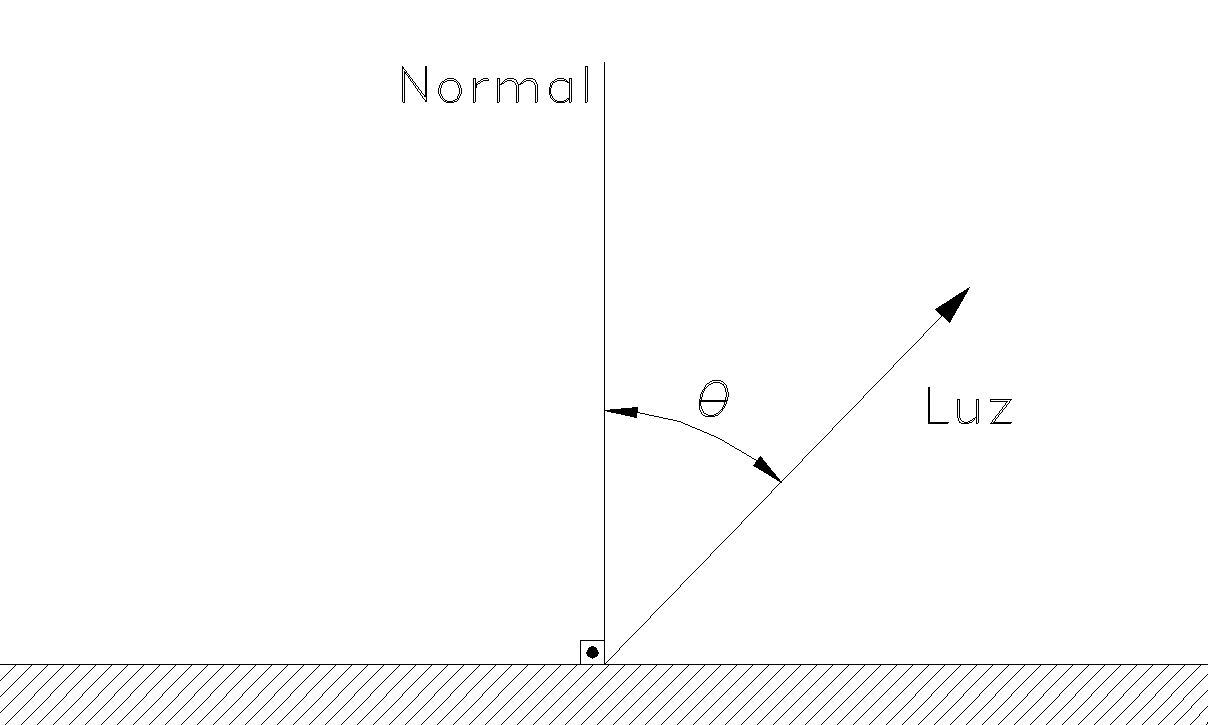
Dirección de la luz respecto a la normal a la superficie
Por lo tanto la cantidad de luz procedente de un punto de la superficie del objeto disminuye con el coseno del ángulo a medida que la superficie gira alejándose de la dirección de visualización. El segundo efecto, que compensa al anterior, es que nosotros no vemos punto sino áreas. A medida que la superficie gira alejándose el número de puntos emisores de luz dentro del área de visión aumenta, y este aumento es precisamente proporcional al inverso del coseno. Por lo tanto, a medida que gira la superficie del objeto, recibimos menos luz desde cada punto, pero estos parecen aproximarse unos a otros, por lo que el efecto conjunto es que la superficie mantiene su brillo.


Una superficie vista de lado aumenta el área productora de luz
Una cancelación similar ocurre si el objeto se aleja desde el observador. La luz procedente de su superficie se reparte sobre área mayor, que crece con el cuadrado de la distancia, por lo que la luz que llega a nuestro ojo disminuye en el mismo factor. Aplicando el mismo razonamiento que antes, aunque al ojo llega menos luz, lo hace sobre un área más pequeña de la retina y el brillo del objeto no varía.
Podemos dar ahora una expresión para el brillo de un objeto iluminado por una luz difusa de fondo. Si F es la intensidad de la luz de fondo y R es la reflectividad del objeto, entonces la intensidad de la luz que procede de su superficie visible será
![]()
Si podemos modificar los valores de F y R, podemos pintar nuestro objeto con diferentes tonos de gris. Pero en este sencillo modelo, cualquier plano de un determinado objeto tendrá el mismo color. Sin embargo, este no es el aspecto real de objeto, para obtener un coloreado más realista debemos incluir también las fuentes puntuales de luz.
Las fuentes de luz puntual son abstracciones de las fuentes reales de luz como las bombillas, las velas o el propio Sol. La luz se origina en un determinado lugar, proviene de una dirección determinada desde una distancia determinada. Para las fuentes puntuales, la posición y la orientación relativa de la superficie del objeto determinara cuanta luz recibirá y, como consecuencia de esto, que brillo tendrá. Las superficies que miren hacia la luz y que estén situadas más cerca de la fuente recibirán más luz que las superficies que estén orientadas en dirección opuesta o se encuentren más lejos de la luz.

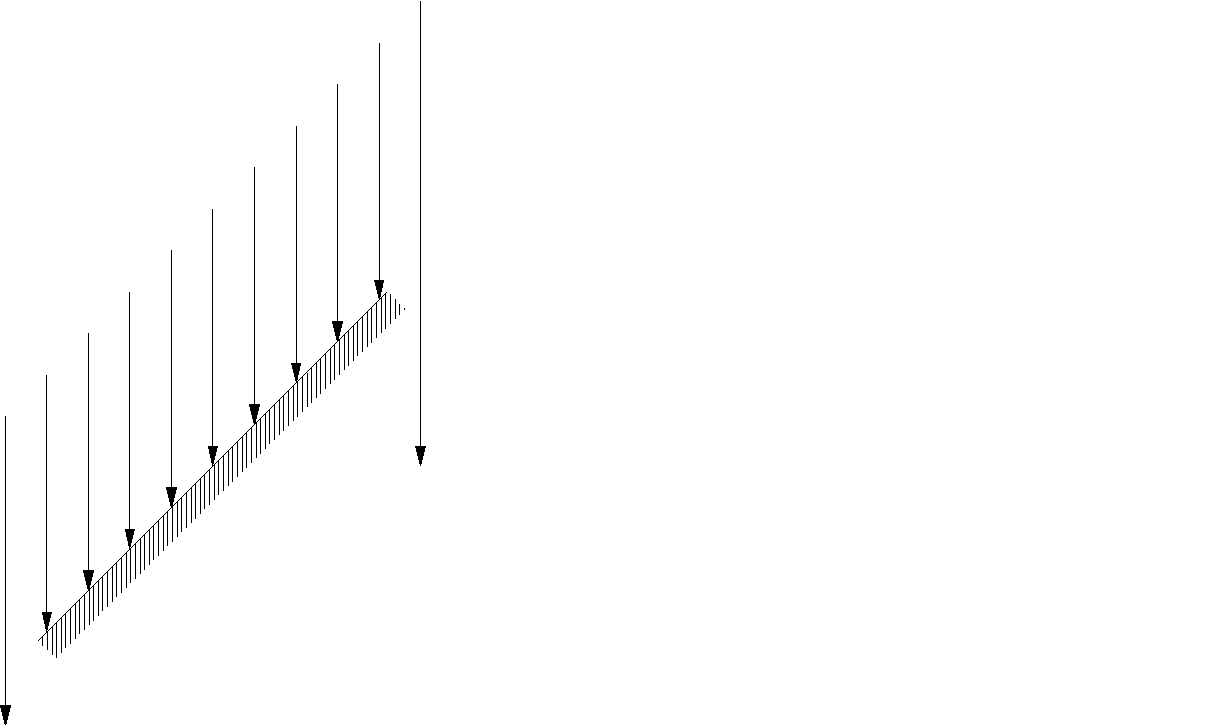
Una superficie perpendicular recibe más luz que otra que forme un ángulo
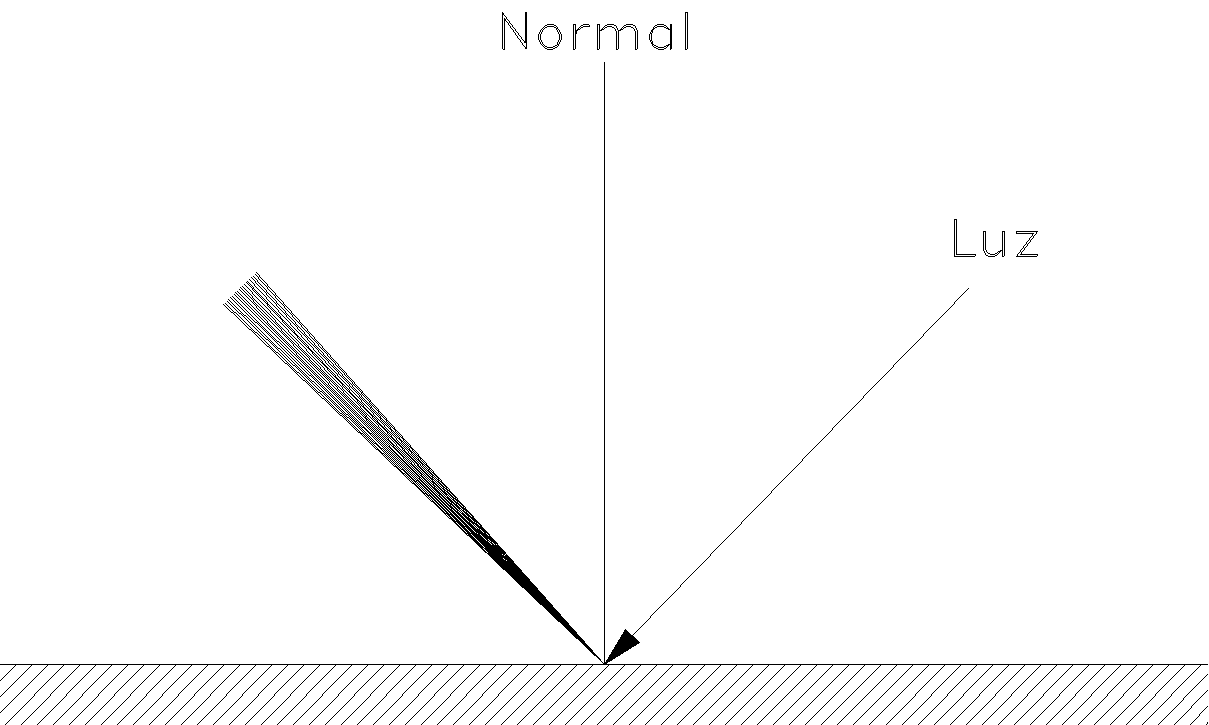
Empecemos considerando los efectos de la orientación. Utilizando argumentos similares a los del capítulo anterior, sabemos que la superficie, a medida que gira alejándose de la dirección de la luz, aparece menos brillante. La iluminación disminuye con el coseno del ángulo a
que forma la normal a la superficie y la dirección de luz incidente. Este ángulo recibe el nombre de ángulo de incidencia.
Ángulo de Incidencia
Si tenemos un vector L de longitud unidad apuntado hacia la fuente de luz y un vector N de longitud unidad en la dirección normal a la superficie, entonces el producto escalar de estos dos vectores es
![]()
Supongamos que P es la cantidad de luz que proviene de la luz puntual, entonces el tono de una cara determinada de un objeto será
![]()
Nuestro modelo puede ser mejorado todavía más. La luz es reflejada por los objetos de dos formas: existe una reflexión difusa, que hemos tenido en cuenta antes, y existe la reflexión especular. La reflexión difusa sólo depende del ángulo de incidencia, pudiendo la luz reflejada tener un color determinado, ya que interviene el coeficiente de reflexión. La reflexión especular actúa de una forma diferente. Es el tipo de reflexión que se produce en un espejo. Toda la luz es reflejada, no solamente algunos colores, y lo hace en una dirección casi única, no en todas las direcciones como establecía la ley de Lambert. Para la reflexión especular, la luz llega, alcanza la superficie y rebota. El ángulo b
que forma el rayo reflejado con la normal a la superficie recibe el nombre de ángulo de reflexión y tiene una magnitud igual al ángulo de incidencia.La luz procedente de una reflexión especular puede observarse cuando la dirección desde el objeto al ojo del observador es la misma que la dirección de la luz reflejada. Otra forma de expresar esto es forma un vector a medio camino entre la dirección de la luz incidente y la dirección del observador. Si comparamos este vector con la normal a la superficie, situado a mitad de camino entre el rayo incidente y el rayo reflejado, cuando coinciden el observador puede ver la luz reflejada.

Reflexión Especular
Si L es el vector de longitud unidad en la dirección del rayo incidente pero saliendo de la superficie y E es el vector unitario en la dirección del observador, entonces
![]()
será un vector unitario a medio camino entre ambos.
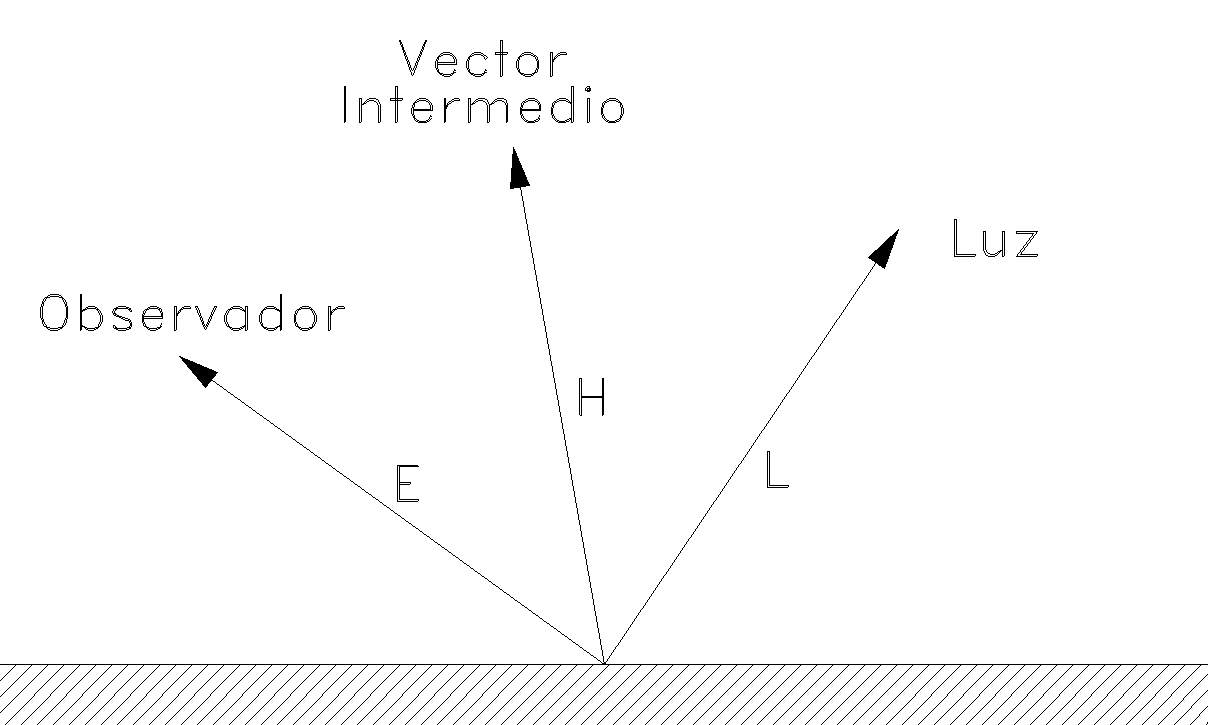
Vector intermedio entre la fuente de luz y el observador
Si N es el vector unitario normal a la superficie, el producto escalar de estos dos vectores nos dará el coseno del ángulo que forman. Cuando la reflexión puede verse, el ángulo entre estos dos vectores será casi nulo y, por lo tanto, su coseno estará próximo a 1.
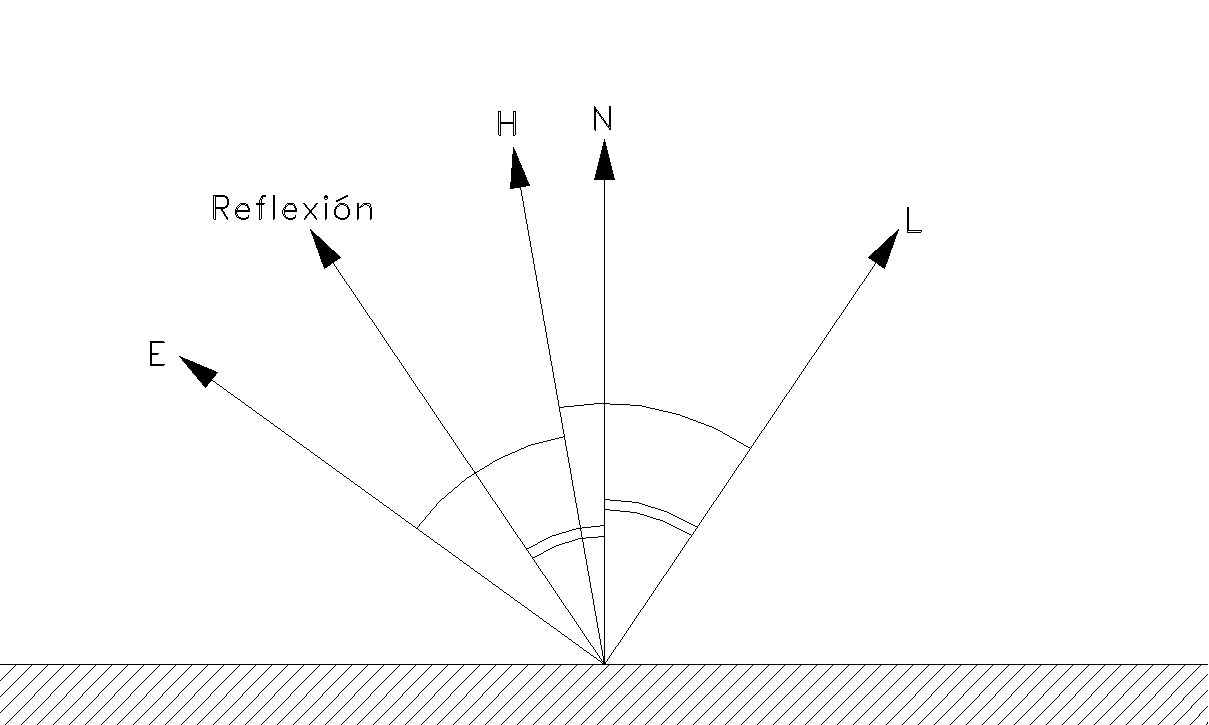
Vectores empleados para la determinacióan de lo que el ojo en la reflexión
Necesitamos entonces una función que valga 1 cuando podemos ver la luz reflejada, pero cae rápidamente hasta 0 para cualquier otro ángulo. Esto puede conseguirse elevando el coseno a una potencia grande.
![]()
El valor de a determina la brillantez de un objeto. Cuando la potencia es elevada se obtiene un efecto especular muy brillante.

Efecto de la potencia de a
: a grande (izquierda) y a pequeña (derecha)Si la cantidad de luz reflejada especularmente es S, entonces nuestra función mejorar de sombreado será
![]()
La cantidad de luz reflejada puede depender del valor del ángulo de incidencia. De hecho el parámetro S debería ser una función de a. Esta puede ser una función complicada que varía con el tipo de material. Para simplificar nuestro modelo, consideraremos, sin embargo, que es constante para cada objeto. Incluida en S está la potencia de la luz puntual P.
Por último, debemos tener en cuenta el efecto de la distancia. En teoría, la iluminación procedente de una fuente de luz puntual debería disminuir con el cuadrado de la distancia entre esta y el objeto. Utilizando esta relación, sin embargo, parece que se produce un cambio demasiado grande con la distancia. Quizás sea debido en parte al hecho de que las fuentes de luz puntual son más grandes que un simple punto. Un objeto iluminado por una luz muy grande cercana a él no mostrará apenas un cambio en la iluminación para pequeños cambios de la distancia. En cualquier caso, necesitamos una función que disminuya con la distancia, pero menos rápidamente que el inverso del cuadrado. Y también queremos acercarnos a un límite finito para pequeñas distancias, de tal forma que no sea necesario preocuparse por las divisiones por cero cuando una fuente de luz esta mal colocada.
Se propone la siguiente función
![]()
donde C es una constante y D es la distancia desde la fuente de luz al objeto.
Nuestra función de sombreado se convierte es
![]()
o de forma generalizada para varias fuentes de luz
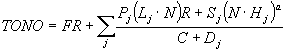
Algunas de las propiedades que no han sido incluidas en este trabajo son las transparencias y las sombras. El efecto de transparencia se consigue mostrando parte de la luz procedente de un objeto oculto. Cuanto mayor es el porcentaje de luz que se deja pasar a través del objeto, más transparente es. Para incluir objetos transparentes en nuestro modelo sería necesario modificar el algoritmo del pintor de tal forma que atenuase el color de un objeto cuando dibujamos otro encima, en vez de eliminarlo por completo, para luego añadir la luz procedente del segundo.
El problema de las sombras es muy parecido al problema de la superficies ocultas. Un objeto sombreado es uno que no recibe directamente la luz pero que está en nuestra línea de visión. Los cálculos necesarios para determinar las superficies ocultas y las sombreadas se suelen realizar simultáneamente por eficiencia. Sin embargo, para poder realizar este proceso es necesario un planteamiento distinto del algoritmo del pintor que nosotros hemos visto para las superficies ocultas. Para tener en cuenta las sombras, es necesario identificar las porciones de las superficies que están a la sombra de un objeto y no sólo eliminarlas.