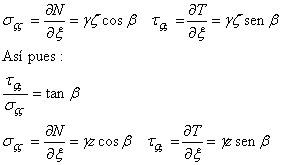Solución al ejercicio 2:

1) Enunciado:

En un terreno semiinfinito con una pendiente 3:10, que se encuentra seco y cuyo peso específico aparente es γ= 20 kN/m³, módulo de elasticidad E=10000kPa y módulo de Poisson ν=0,4 se pide:

Se pide:

1) Obtener la tensión normal y cortante sobre un plano paralelo a la superficie del terreno a una profundidad de 3m.

2) Obtener la distribución de presión normal y cortante sobre un plano perpendicular a la superficie del terreno y las correspondientes a 3m de profundidad.

3) Idem para un plano vertical.

4) Obtener las tensiones principales y la dirección de las mismas a 3m de profundidad.

2) Solución:

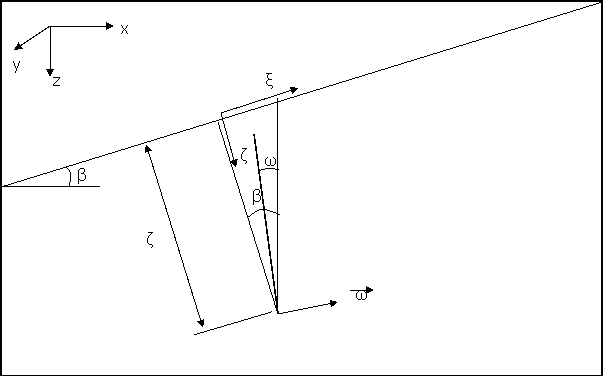
Tomemos el sistema de referencia absoluta xyz de la figura y otro sistema de referencia ξyζ, en el que mantenemos el eje OY y giramos el plano xz de forma que los ejes resulten paralelos a la superficie del terreno.

Se trata de un estado de deformación plana, pues las cargas y las fuerzas internas actuantes son todas normales al eje OY y los desplazamientos en este eje son nulos. Por consiguiente:

Y empleando las leyes de Hooke se puede deducir:

Cojamos una franja de terreno en la dirección normal a la superficie, de ancho dξ y alto ζ correspondiente a una profundidad z, y dibujemos las fuerzas que actúan sobre la base paralela a la superfice, tal y como se muestra en la Figura 1.

Figura 1.- Fuerzas actuantes en una franja de terreno.

Si establecemos el equilibrio de fuerzas según las direcciones normal y tangencial a la base:

(1)

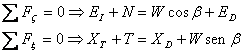
Por ser un sólido semiinfinito, cualquier plano perpendicular al eje ξ está sometido a las mismas fuerzas, ya que el estado tensional es independiente de ξ, en consecuencia:

(2)

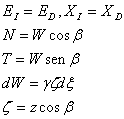
Ahora bien, los esfuerzos en la base de la franja de terreno, paralela a la superficie, serán el resultado de dividir las fuerzas por el área:

(3)

Lo cuál nos proporciona las tensiones existentes sobre un plano paralelo a la superficie del terreno y a una profundidad z estando la tensión cortante y el esfuerzo normal relacionados por la tangente del ángulo de inclinación del terreno independientemente de la profundidad.

Ahora nos proponemos obtener las tensiones sobre un plano perpendicular a la superficie del terreno, es decir, perpendicular a ξ.

Para ello tengamos en cuenta que los desplazamientos para todos los puntos situados en un plano paralelo a la superficie del terreno, son iguales, por ser el terreno semiinfinito, es decir, que son independientes de y y de ξ: (estado de deformación plana):

(4)

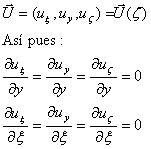
En el tensor de deformaciones tendremos por consiguiente:

(5)

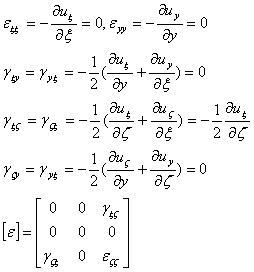
Aplicando las leyes de Hooke tenemos:

(6)

Por consiguiente en un plano normal a la superficie no hay deformación de compresión, únicamente distorsión angular en el plano normal a OY.

Operando y teniendo en cuenta (1) y (1) 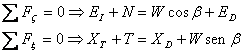(3) se tiene:

(7)

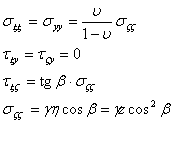
Y por consiguiente podremos expresar el tensor de tensiones referido a los ejes ξyζ como:

(8)

En cuanto al tensor de deformaciones obtenido en (5), si aplicamos lo obtenido (6) de las leyes de Hooke y las relaciones (7) tendremos:

(9)

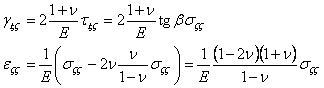
Y por tanto el tensor de deformaciones podremos escribirlo referido a ejes ξyζ como:

(10)

Estamos ahora en disposición para contestar algunas de las preguntas:

1) Obtener la tensión normal y cortante sobre un plano paralelo a la superficie del terreno a una profundidad de 3m

Un plano paralelo a la superficie del terreno vendrá representado en ejes ξyζ por el vector :

En nuestro caso . Así pues:

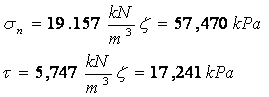
2) Obtener la distribución de presión normal y cortante sobre un plano perpendicular a la superficie del terreno y las correspondientes a 3m de profundidad.

El vector normal al plano es y por consiguiente:

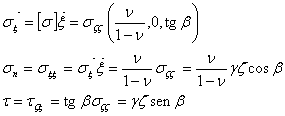
Que para el caso particular del ejercicio, nos proporciona:

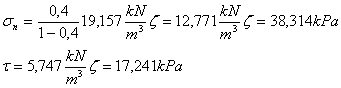
3) Idem para un plano vertical.

Obtengamos la presión normal y cortante sobre un plano inclinado un ángulo ω respecto a la vertical.

Figura 2 Plano inclinado un ángulo ω respecto a la vertical.

Las coordenadas del vector normal al plano referido a ejes ξyζ vendrán dadas por (ver Figura 2):

Y en definitiva:

Para el caso de un plano vertical, ω=0 y por tanto

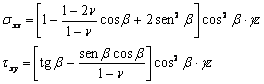
4) Obtener las tensiones principales y la dirección de las mismas a 3m de profundidad.

Por ser un caso de deformación plana, y por consiguiente uno de los ejes principales será OY, en el que la tensión principal vendrá dada por:

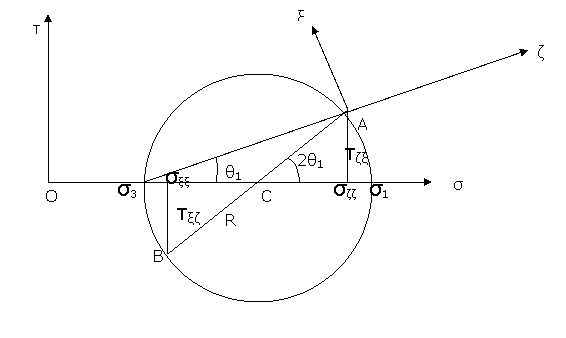
Figura 3 Obtención de las tensiones principales

En la Figura 3 se representa el círculo de mohr correspondiente a un punto del terreno a una profundidad z. El punto A representa el estado tensional en un plano paralelo a la superficie del terreno, que estará sometido a esfuerzo cortante τ_{ζξ y tensión normal} σ_ζζ. El punto B representa un plano perpendicular a la superficie del terreno, que forma 90º con el anterior y por tanto estará diametralmente opuesto al punto A en el círulo de mohr. Este plano estará sometido a esfuerzo cortante τ_ξζ y tensión normal σ_ξξ.

Según se deduce de la figura:

(11)

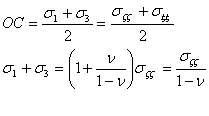
(12)

Sumando las ecuaciones (11) y (12) obtenemos el valor de la tensión principal máxima, y restando la (12) de la (11) obtenemos la tensión principal mínima:

(13)

Y si lo ponemos en función de la profundidad z observaremos que las tensiones principales aumentan también (como era de esperar) linealmente con la profundidad:

(14)

Podemos ahora comprobar que, efectivamente, la tensión principal mínima es la obtenida y que es menor que la obtenida para la dirección OY:

(15)

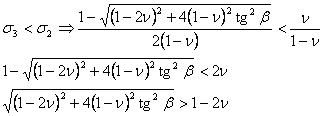
Lo cual es cierto para cualquier valor de ν, y por consiguiente OY es el eje principal intermedio.

Del la Figura 3 podremos obtener también el ángulo que forma la dirección principal máxima con la normal a la superficie del terreno:

(16)

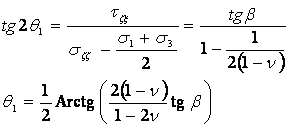
Como se puede observar, la dirección de los ejes principales es independiente de la profundidad o del módulo edométrico, sólo depende de la inclinación del terreno y del módulo de poisson.

El ángulo que forma la dirección principal máxima con respecto a la vertical (verFigura 4) vendrá dado por:

(17)

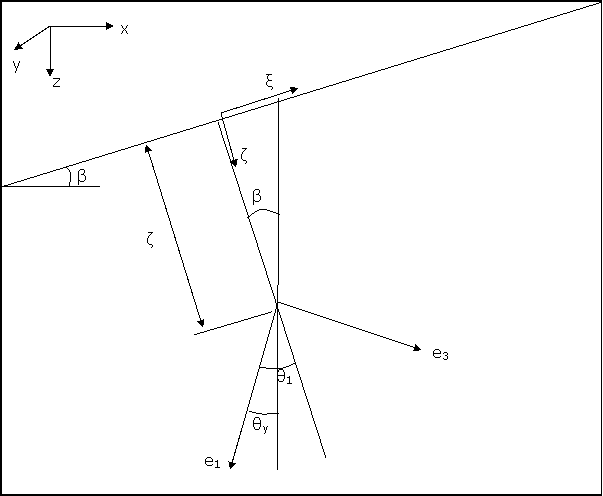
Figura 4 Dirección de las tensiones principales