Solución al ejercicio 1:
Enunciado:
Un estrato de terreno horizontal de 5m de potencia descansa sobre una roca dura. El terreno se encuentra seco y su características son: peso específico aparente γ= 20 kN/m3, módulo de elasticidad E=10000kPa y módulo de Poisson ν=0,4.
Se pide:
1) Obtener la distribución de presiones verticales en el terreno.
2) Obtener la distribución de presiones horizontales.
3) Evaluar la influencia del módulo de Poisson y del módulo de elasticidad.
4) Obtener las deformaciones elásticas verticales sufridas por el terreno bajo su propio peso.
5) Obtener los desplazamientos en superficie debidos a las deformaciones bajo su propio peso..
Solución:
Cojamos una franja de terreno de ancho x y profundidad z, y
dibujemos las fuerzas que actúan sobre la base horizontal tal y como se muestra
en
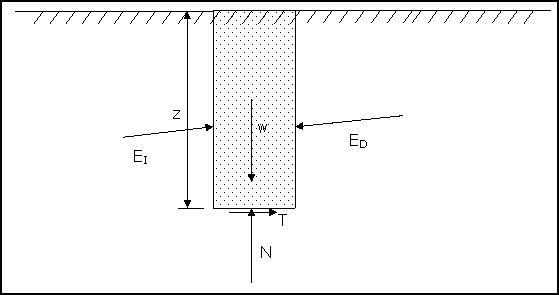
Figura 1.- Fuerzas actuantes en una franja de terreno.
Si establecemos el equilibrio de fuerzas normales y paralelas a la base, podremos establecer:
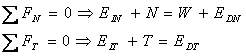
Dado que el terreno es indefinido en la dirección horizontal, el estado tensional en dos planos verticales cualesquiera ha de ser el mismo, y por tanto las fuerzas actuantes sobre las caras izquierda y derecha de la franja serán iguales y de sentido contrario (por principio de acción y reacción). Así pues, podremos establecer:
Ahora bien, el peso de la franja vertical de terreno será: 
y la presión vertical (σv) y la fuerza
cortante (τv) sobre el plano horizontal serán pues:
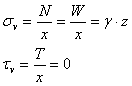
En consecuencia, la presión vertical sobre un plano horizontal será igual al peso de la columna de terreno que tiene por encima y el cortante será nulo.
En consecuencia cualquier plano horizontal es plano principal y la dirección vertical será principal. Por ello, los planos verticales (y la dirección horizontal) serán también principales, y las presiones sobre un plano vertical serán horizontales.
En un material elástico isótropo, las direcciones principales de deformación coincidirán con las de tensiones.
Al no existir ninguna fuerza con componentes horizontales,
los corrimientos en la dirección horizontal serán nulos y en consecuencia se
puede deducir 
y estaremos en
un caso de deformación axial, es decir, un plano vertical no está sometido a
deformaciones, únicamente los planos horizontales están sometidos a compresión
normal.
Si tenemos en cuenta las leyes de Hooke y aplicacmos lo anterior tendremo:
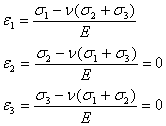
De donde podemos establecer:
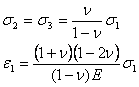
En un punto del terreno, a la relación entre la presión
horizontal y vertical se la conoce como empuje de tierras en reposo y se la
denota como K0. Así pues, para un terreno semiinfinito horizontal
con comportamiento elástico, podemos establecer 
.
La solución a las preguntas del ejercicio ha de ser:
1) La
distribución de presiones verticales (sobre un plano horizontal) serán normales
al plano y siguiendo una ley lineal dada por: 
.
Para 5m de profundidad la presión vertical es de 100kPa.
2) La
distribución de presiones horizontales (sobre un plano vertical) serán normales
al plano y siguiendo una ley lineal dada por: 
.
Para 5m de profundidad la presión horizontal es de 66,67kPa.
3) El módulo de elasticidad no influye en la distribución de presiones, ya que el coeficiente K0 sólo depende del de Poisson. El módulo de Poisson influye en la relación entre la presión horizontal y la vertical.
4) Las
deformaciones unitarias en una dirección horizontal son cero, por lo que no hay
desplazamiento horizontales. En la dirección vertical no son cero, pero es
dirección principal, con lo que los desplazamiento sólo serán en la dirección
vertical. La deformación unitaria aumenta linealmente con la profundidad según
la expresión: 
. Para 5m de profundidad, la deformación unitaria será
de 4,6710-3.
5) Los
desplazamiento verticales serán el resultado de integrar las deformaciones
unitarias: 
.
Los desplazamientos en superficie serán pues de u(0)= 11.67 mm.
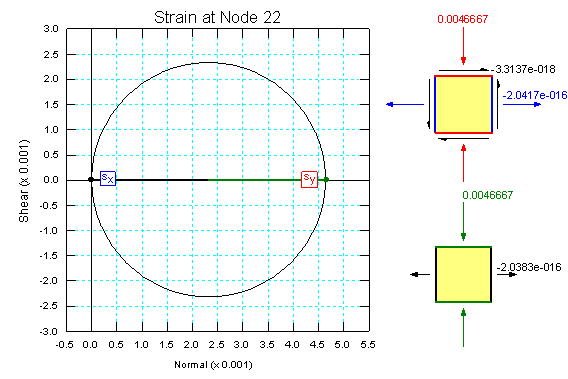
La modelización del Sigma/W arroja las siguientes gráficas para una línea vertical que concuerdan perfectamente con lo obtenido de forma analítica.
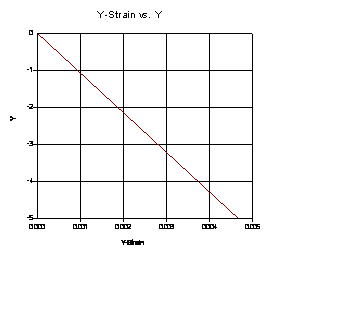
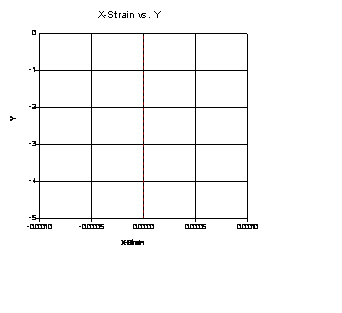
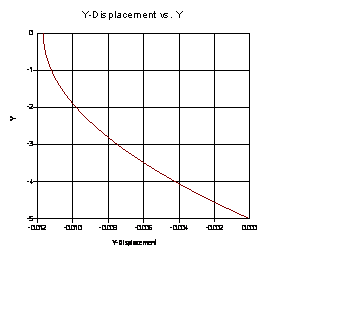
El tensor de tensionesobtenido para el punto 5m de profundidad es:
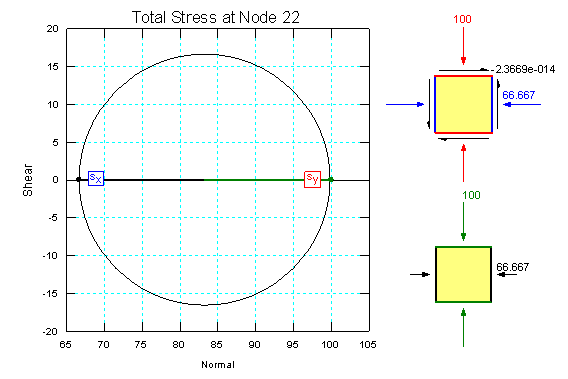
Y el de deformaciones:
