Solución al Ejercicio 1
Para obtener la solución se han llevado a cabo los siguientes pasos:
- se ha definido la función de coeficiente del permeabilidad con una permeabilidad constante dando dos valores iguales para una presión de poro 0 y otro valor positivo cualquiera. Tener en cuenta que, si bien K nos la proporcionan en cm/s, en el programa ha de ser introducida en m/s, ya que hemos seleccionado los m como unidad de longitud.
- Se ha definido un material al que se le ha asignado la función anterior como función de permeabilidad.
- Se ha creado una malla fina de manera que en los límites de la cortina de la presa exista siempre un nodo (como se puede ver en la solución).
- Se han asignado las condiciones de contorno: altura de presión de 8m (o altura total de 20m, que sería equivalente) en los nodos de la superficie aguas arriba de la presa. Altura de presión 0m (o 12m de altura de carga total) en los nodos de la superficie aguas debajo de la presa. En los nodos bajo la cortina de la presa y en los de los laterales y el fondo de la zona de material modelizada se ha empleado una condición de contorno de flujo total 0, ya que si estamos suficientemente alejados de la presa, no hay circulación de agua por se las condiciones hidrostáticas.
- Se ha verificado el modelo.
- Se ha calculado.
- Por último se procede a la visualización de restultados.
1) Distribución de velocidades, altura de carga hidráulica y de columna de presión del agua que se infiltra en el terreno de cimentación.
En
Observamos que la circulación es descendente en las cercanías de la presa aguas arriba de la misma, subparalela a la base de la misma por debajo, y ascendente en la zona cercana a la presa aguas abajo de la misma, siendo además en esta zona donde la velocidad es máxima. Al haber velocidades ascendentes elevadas, se corre el riesgo de llegar al sifonamiento en esta zona, por aumento de la presión de filtración. Ello tiene como consecuencia una reducción de la resistencia cortante del terreno (al hallarse a menores presiones efectivas que en condiciones hidrostáticas) que puede poner en peligro la estabilidad de la presa. Para resolver este problema se suele poner un enrocamiento o un dren de grava en la puntera de la presa.
En cuanto a la distribución de altura de carga hidráulica, vemos que tiene una distribución en abanico, oscilando entre 12 y 20m como era de esperar. Observar que las lineas de corriente son ortogonales a las de equipotencial hidráulico. Como era de esperar, por las condiciones de contorno impuestas, flujo bajo la cortina de la presa el paralelo a la base, ya que hemos impuesto que la base sea impermeable y por tanto una línea de corriente. Los límites del terreno también son una línea de corriente, y en sus cercanías la velocidad de flujo es prácticamente cero. Por último, en la superficie del terreno bajo el agua, la altura de carga es de 20m y por delante de la presa, de 12.
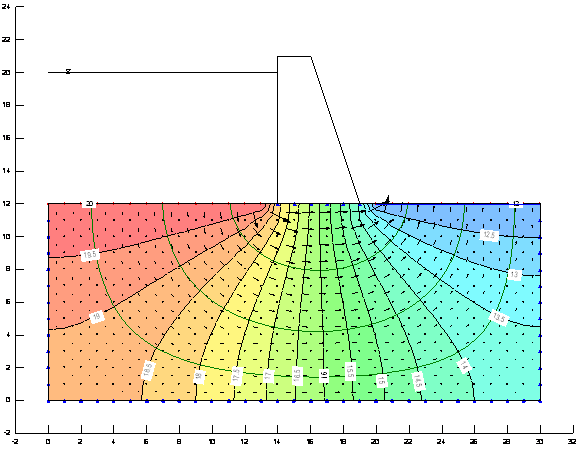
Ilustración 1 Distibucion de velocidades y alturas de carga.
En la Ilustración 1Ilustración 2 se encuentra representada la distribución de columnas de presión del agua. Observar que en los extremos derecho e izquierdo la distribución de presiones es aproximadamente la hidrostática, ya que no hay prácticamente circulación de agua, pasando progresivamente de una a otra en los planos intermedios.
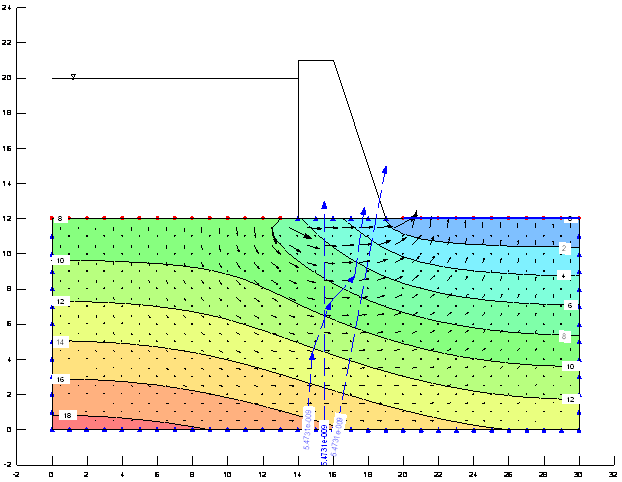
Ilustración 2 Distribución de la altura de presión.
2) Caudal que se escapa por el terreno bajo la presa.
El empleo de una sección de flujo (‘flux section’) que corta todas la líneas de flujo en el material modelizado (ver Ilustración 2), nos permite estimar el caudal de agua que se escapa bajo la presa que es de unos 5,47 10-9 m3/s por metro longitudinal de presa, es decir unos 172,5 l/año por metro longitudinal de presa.
Obsérvese que aunque la sección empleada varíe de dirección o de forma, el caudal obtenido es el mismo, siempre y cuando se corten todas las líneas de flujo.
1) ¿Cómo diferirá el flujo de agua si el terreno se sustituye por otro de K=10-5cm/s? ¿Sufrirá variaciones la distribución de carga hidráulica? ¿y las velocidades?
En el caso de un flujo estacionario y en
un material homogéneo, la ecuación de continuidad del flujo queda reducida a la
ecuación de Laplace ![]() que igualmente podría escribirse
como
que igualmente podría escribirse
como ![]() , por lo que la distribución de
alturas de carga resultantes depende únicamente de las condiciones de contorno
y no de la permeabilidad del material.
, por lo que la distribución de
alturas de carga resultantes depende únicamente de las condiciones de contorno
y no de la permeabilidad del material.
Por ello la distribución de alturas de carga y de presión del agua es la misma que en el caso 1 (como se puede observar en la Ilustración 3y en la Ilustración 4).
La distribución de la velocidad es
aparentemente la misma al caso anterior, si bien hay que tener en cuenta que se
ha cambiado el factor de amplificación que ahora es de 107, ya que
en caso de usar el mismo factor (109) las flechas resultarían
excesivamente grandes. Por eso, en estas ilustraciones una flecha del mismo
tamaño corresponde a una velocidad cien veces mayor. La velocidad máxima ahora
es de 1,5 10-5 cm/s, es decir 100 veces mayor, como corresponde
proporcionalmente al aumento de permeabilidad y como cabría esperar de la ley
de Darcy (![]() ) ya que la distribución de alturas
de carga es la misma.
) ya que la distribución de alturas
de carga es la misma.
Como el campo de velocidades es nomotético del anterior con un factor de 100, el caudal es también 100 veces superior, es decir 5,47 10-7 m3/s.
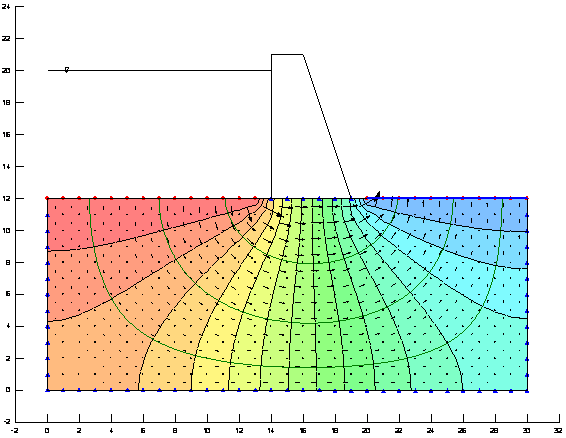
Ilustración 3 Distribución de altura de carga y velocidades con K=10-5 cm/s
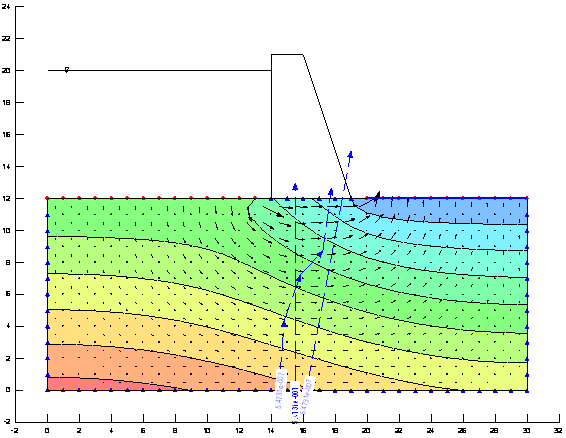
Ilustración 4 Distribución del presiones con K=10-5 cm/S